1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
동적 계획법?
잘 알려져 있는 동적 계획법(Dynamic Programming) 문제이다. 동적 계획법은 큰 문제를 여러 개의 작은 문제로 나누어 푸는 방법을 의미한다고 생각하면 편하다. 각 하위 문제를 해결한 후 그 해결에서 얻은 답을 나중에 다시 사용하는 방법인 것이다. 이 꼬리의 꼬리를 무는 과정을 계속하다 보면 결국 우리가 원하는 큰 문제에 대한 답이 튀어나온다는 원리인 것이다.
가장 좋은 예시로는 피보나치 수열이다. 9 번째 피보나치 수열의 값을 얻기 위해서는 0+1=1 -> 1+1=2 -> 1+2=3....처럼 아래에서부터 차근차근 올라가는 과정을 진행에 있어 과거에 구해 놓았던 값을 다시 이용하면 된다.
접근
그렇다면 이 문제를 풀기 위해서는 어떤 접근이 필요할까? 사실 두 가지 풀이가 가능하다.
1. 동적 계획법 이용
아까도 말했듯이 이 알고리즘은 큰 목표를 위해 작은 목표의 답을 구해놓아야한다. 그리고 하위에서 상위로 올라가기 때문에 바텀 업(Bottom-Up) 방식을 따를 것이다.
즉 입력 n을 받으면 2의 답(2->1. 1번)을 1로부터(과거의 흔적) 도출해 내고 3의 답(3->1. 1번)을 마찬가지의 방법으로 도출해 내면서 마찬가지로 k의 답을 내기 위해서 k/3, k/2, k-1의 값을 참고해서 k가 1이 되기 위해 몇 번의 연산이 필요한지 구하면 되는 것이다. 예를 들어 k/3이 4, k/2가 5, k-1이 7의 값이 할당되어 있으면 k는 4, 5, 7의 최솟값인 4를 물려받아 5(4+1)의 값이 할당되는 것이다.
최종 코드>>
import sys
input = sys.stdin.readline
n = int(input())
dp = [0] * (n + 1)
for i in range(2, n + 1):
dp[i] = dp[i - 1] + 1
if i % 3 == 0:
dp[i] = min(dp[i], dp[i // 3] + 1)
if i % 2 == 0:
dp[i] = min(dp[i], dp[i // 2] + 1)
print(dp[n])해석
0으로 초기화 된 dp리스트를 만들어 준다. 크기가 n+1인 이유는 dp [n]=(n에 할당된 값)으로 직접 접근하고 싶기 때문이다. 이렇게 하지 않을 시 dp [n-1]=(n에 할당된 값)으로 접근되기 때문이다.
어차피 dp[1]=0이므로 추가적인 밑 작업 필요 없이 바로 비교 연산 진행을 해주면 된다.
일단 dp[i]=dp[i-1]+1이라고 가정하고 나서 다른 경우들을 살펴보는 것이다.
만약 i가 3으로 나누어 떨어짐에도 불구하고 d [i-1]+1(dp [i]와 동일한 표현)이 dp [i//3]+1보다 작다면 dp [i]의 값은 dp [i-1]이 갱신되지 않은 채 남게 되는 것이다. 물론 2로 나누어 떨어진다는 조건도 무사히 통과했다는 전제에서다. 또한 i%3이 먼저 있든 i%2가 먼저 있든 상관없다!! 어차피 세 가지 경우의 수 중에서 가장 작은 값으로 대체될 것이기 때문이다.
2. 너비 우선 탐색(bfs) 이용
놀랍게도 그래프 탐색으로도 풀 수 있는 문제이다. 동적 계획법은 잠시 옆으로 밀어내고 순수히 이 방법에 대해 생각해보자. 사실 앞에서 생각해 보았던 1 ~ n까지의 모든 값을 배열에 저장하고 문제를 푸는 것은 비효율적일 수도 있다. 왜냐하면 굳이 구할 필요도 없었던 값들까지 포함해서 계산을 했기 때문이다.
하지만 bfs를 이용하면 아래의 그림처럼 불필요한 연산을 많이 줄일 수 있다.
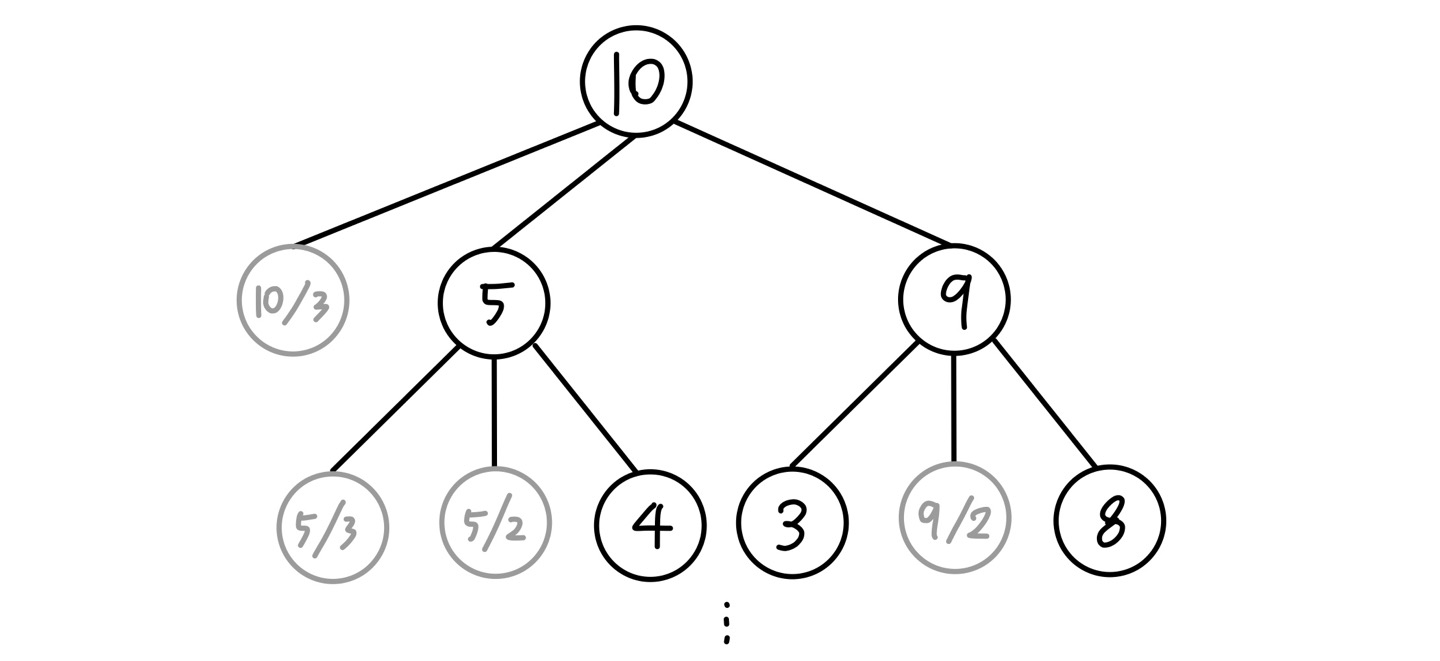
일단 처음부터 dp와 다른 점은 탑 다운(Top-Down) 방식이라는 데에 있다. n에서부터 출발하여 1까지 가장 먼저 도달함을 목적으로 한다.
최종 코드>>
from collections import deque
import sys
input = sys.stdin.readline
n=int(input())
Q=deque([n])
trace=[0]*(n+1)
while Q:
target=Q.popleft()
if target==1:
break
if target%3==0 and not trace[target//3]:
Q.append(target//3)
trace[target//3]=trace[target]+1
if target%2==0 and not trace[target//2]:
Q.append(target//2)
trace[target//2]=trace[target]+1
if not trace[target-1]:
Q.append(target-1)
trace[target-1]=trace[target]+1
print(trace[1])해석
전형적인 bfs 코드이다. 하지만 다소 의아한 점은 trace안에 있는 값들은 절대 바뀌지 않는다. 어찌보면 당연하다. 왜냐하면 먼저 저장된 값은 나중에 들어온 값보다 반드시 작기 때문이다. 4를 예시로 들어보자.
Q에 있던 4가 popleft되어 target으로 저장될 것이다. 이때 조건문들을 거치면 3(4-1)과 2(4/2)가 1로 채워질 것이다.
-> trace = [0, 0, 1, 1, 0]
-> Q = [2, 3]
이제 2가 target이 되고 조건문들을 거치면 1은 2(target%2==0 조건이 먼저 있기 때문에 2-1이 아니라 2/2에 의해 1로 채워짐)로 채워질 것이다.
-> trace = [0, 2, 1, 1, 0]
-> Q = [3, 1]
이제 3이 target이 되고 조건문들을 거치면 2에는 2가 저장되려고 할 것이다. 왜냐하면 네 번째 조건문을 거쳐 3-1을 하면 2에 3에 저장된 값 1과 추가 1이 합해져서 저장돼야 하기 때문이다. 하지만 3에는 이미 1이 저장되어 있고 심지어 1이 2보다 작기 때문에 1이 저장되어야 하는 것이 맞다! 즉 먼저 저장된 값은 반드시 이후에 접근되는 값보다 작다.
bfs도 dp와 마찬가지로 어느 조건문이 먼저 와도 상관 없다.
'백준 > Silver(1~5)' 카테고리의 다른 글
| [백준]_16139번 : 인간-컴퓨터 상호작용(파이썬) (3) | 2023.11.08 |
|---|---|
| [백준]_12852번 : 1로 만들기 2(파이썬) (0) | 2023.10.30 |
| [백준]_1260번 : DFS와 BFS(파이썬 and C언어) (0) | 2023.09.23 |
| [백준]_1931번 : 회의실 배정(파이썬 and C언어) (0) | 2023.08.25 |
| [백준]_2606번 : 바이러스(파이썬 and C언어) (0) | 2023.08.21 |


