Paper :
Presentation content :
Main interest
그래프에서의 link prediction을 주 관심사로 한다. 이는 즉 네트워크가 주어졌을 때 두 노드 사이의 link가 존재 유무를 판별하는 작업이다. 이는 추천 시스템은 물론이고 지식 그래프 completion, 의학 데이터 재구축(e.g., metabolic network, PPI) 등에 사용될 수 있다.

Problem with previous models
그래서 두 노드 사이의 연결을 어떻게 판별할 것인가? 가장 널리 사용된 방법은 휴리스틱을 정의하는 것이다. 휴리스틱이란 두 노드 사이의 link가 이루어질 score를 계산할 수 있는 일종의 함수이다. 즉 입력은 두 노드와 관련된 정보(주변의 구조적 특징, 두 노드로 이어질 수 있는 경로의 개수 등)이며 출력은 두 노드 사이의 link가 존재할 점수이다. 앞으로 그 두 노드를 target 노드라고 하겠다.
이 분야에 대한 초창기 연구들은 "target 노드 사이에 link가 존재할 기준"을 정의하였다. 가령 common neighbors(CN)은 target 노드가 $1$-hop 거리에 공통 이웃이 얼마나 많은지를 기준으로 했고 Katz index는 하나의 target에서 다른 target으로 갈 수 있는 경로의 개수를 link의 기준으로 삼았다.
즉 모델은 target을 중심으로 몇 hop까지 사용할 것이냐로 분류할 수 있다. 즉 $k$-hop까지의 정보를 사용하는 휴리스틱은 k-order 휴리스틱이라고 할 수 있다. 추가로 네트워크 전체의 정보가 필요한 high-order 휴리스틱 또한 존재하며 Katz index가 이에 해당된다. 또한 target 주변의 노드들을 관찰한다는 것은 일종의 local subgraph를 샘플링한다고 볼 수 있다.

하지만 이러한 pre-defined 휴리스틱은 문제가 하나 있다. 정의하 휴리스틱이 모든 네트워크에서 일반적으로 적용되리라는 보장이 없다. 예를 들어 common neighbor 휴리스틱은 소셜 네트워크에서는 옳을지 몰라도 PPI 네트워크에서는 공유 이웃이 많을수록 상호작용할(link가 존재할) 확률이 덜하다고 한다.
그렇다면 입력 네트워크가 주어졌을 때 그 네트워크만의 특성을 학습해 link를 예측할 수 있는 일반적인 모델이 필요할 것이다. 앞서 살펴보았던 사전에 정의된 휴리스틱을 사용하지 않고 '입력 네트워크에 가장 적절한 휴리스틱'을 학습할 수 있는 모델을 만드는 것이다. 이에 연구는 WLNM(KDD, 2017)에서 최초로 진행되었고 상당한 성능 향상에 기여하였다.
WLNM은 Weisfeiler-Lehman 알고리즘에 기반한 모델이다. 이 알고리즘은 두 그래프가 isomorphic한지 확인하는 알고리즘이다.
하지만 WLNM에는 문제점이 몇 가지 있다.
1. 샘플링 한 subgraph에 대해 fully connected layer를 사용하므로 고정 된 크기의 입력만 받을 수 있다. 이는 다른 크기의 subgraph도 동일한 크기로 잘라야 하기 때문에 구조적 정보를 잃을 위험이 있다. WLNM의 경우 subgraph를 샘플링할 때 특정 hop만큼 보는 것이 아니라 subgraph에 노드의 개수가 $K$개 이상이 될때까지 hop을 증가시킨다. 이때 $K$는 하이퍼 파라미터이다.
2. Latent, explicit feature 로부터 학습할 수 없다. 이는 subgraph의 인접 행렬로만 학습이 이루어지기 때문에 그래프의 더 다양한 특성들을 학습할 수 있는 기회를 놓친다.
3. 이론적 정당화의 부제가 있다.
이외에도 비슷한 계열의 연구로 서로 다른 휴리스틱 조합들을 지도 학습 모델로 학습하는 시도가 있었지만 여전히 사전 정의된 휴리스틱에 의존하기 때문에 일반화 문제가 여전하다.
이러한 문제들을 해결하기 위해 SEAL이 제안되었다. SEAL은 $\gamma$-decaying 휴리스틱을 정의하고 입력 네트워크에 가장 적절한 휴리스틱을 학습한다. WLNM과는 다르게 SEAL은 fully connected neural network를 GNN(정확히는 DGCNN)으로 대체해 고정 크기 입력 문제를 해결하고 subgraph의 정보뿐만 아니라 latent, explicit 노드 특성들까지 학습에 사용하여 더 다양한 표현력을 갖춘 모델 기반이 된다. 또한 모델의 구조와는 별개로 local subgraph로 충분히 link prediction을 수행할 수 있는 충분한 정보가 담겨 있음을 이론적으로 제시한다.
Architecture
먼저 휴리스틱에 대한 이론을 소개하겠다. 이 이론은 다양한 휴리스틱들이 하나의 일반적인 $\gamma$-decaying 휴리스틱으로 통합될 수 있음을 보인다. 물론 오차가 존재하지만 그 오차도 subgraph의 hop 수에 따라 기하급수적으로 감소함을 보인다.
기호 정리
$G=(V,E)$는 무방향 그래프, $V$는 노드 집합, $E\subseteq V\times V$는 존재하는 link 집합이다. 노드 $i$와 노드 $j$ 사이에 link가 존재하면 1($(i,j)\in E$), 아니면 0($(i,j)\notin E$)의 값($A_{i,j}$)을 갖는 인접 행렬 $A$, 어떤 노드 $x,y$에 대해 $\Gamma(x)$는 $x$의 $1$-hop 거리 이웃 집합, $d(x,y)$는 두 노드 사이의 최단 거리이다. 마지막으로 $w=\left<v_0,\cdots ,v_k \right>$는 $v_0$ 노드에서 $v_k$까지 link를 타고 갈 수 있는 walk이며 $|\left<v_0,\cdots ,v_k \right>|$는 walk의 길이이다(이 경우 $k$).
휴리스틱 통합 이론
먼저 subgraph의 정의는 다음과 같다.

즉 $h$-hop subgraph에 대한 정보는 전부 $G_{x,y}^h$에 들어있다는 것이다. 여기서 두 노드 $x,y$는 link가 존재하지 않아도 subgraph를 아래와 같이 구축할 수 있다.

그래서 결국 보여주고자 하는 것은 $h$가 일정 크기 이상이 되면 high-order 휴리스틱만큼의 표현력을 갖출 수 있다는 것이다.

$\gamma$는 $0<\gamma<1$인 decaying factor이고 $\eta$는 양의 상수 또는 상한이 존재하는 $\gamma$에 대한 양함수이다. $f$는 네트워크에서 주어진 $x,y,l$(target 노드 2개, walk의 길이)에 대한 양함수이다.

Theorem 2에 의하면 2개의 property를 $f$가 만족하면 $\gamma$-decaying 휴리스틱은 $G_{x,y}^h$로부터 근사 가능하다.
각 property를 풀어서 써보자면 다음과 같다.
property 1 : $f$의 상한이 존재
property 2 : 자연수 $h$에 대한 아핀 변환 형태의 walk 길이까지 $G_{x,y}^h$로부터 계산 가능
기하급수적 감소 오차 증명은 아래와 같다.

근사 표현식에서 property 2가, 첫 부등식에서 property 1이 각각 사용되었다. 즉 $0<\gamma \lambda<1$을 만족시키는 한 오차는 $h$에 따라 기하급수적으로 감소한다.
다음으로 3개의 대표적인 high-order 휴리스틱(Katz index, PageRank, SimRank)들이 $\gamma$-decay 휴리스틱의 부분임을 증명한다. 증명은 논문에 자세히 나와있기 때문에 여기서는 생략한다.
이를 통해서 우리가 알 수 있는 것은 대부분의 high-order 휴리스틱이 효과적으로 $h$-hop subgraph로부터 근사될 수 있다는 것이다. 이러한 통합성은 우연이 아니라고 저자들은 주장한다. 왜냐하면 hop의 수가 커질수록 그 hop에 해당하는 정보들의 중요도가 지수적으로 감소하는 것이 직관적으로 자연스럽기 때문이다.
구체적 구조
3개의 부분으로 나뉜다. 1) subgraph 추출, 2) 노드 정보 행렬 구축, 3) GNN 학습.네트워크가 주어졌을 때 SEAL은 자동적으로 휴리스틱을 학습한다. 따라서 기존의 pre-defined 휴리스틱과 비교했을 때 다양한 그래프에 적용성 범위가 넓고 일반화가 잘된다.

GNN은 전형적으로 $(A, X)$를 입력 받는다. $A$는 subgraph의 인접 행렬이고 $X$는 각 subgraph에 따라 해당하는 노드 정보 행렬이다. $X$는 3가지로 구성된다 : 1) 구조적 노드 라벨, 2) 노드 임베딩, 3) 노드 특성.
1) 구조적 노드 라벨
노드 라벨링 함수 $f_l:V\rightarrow \mathbb{N}$는 subgraph에 있는 모든 노드에 대해 정수 라벨을 매겨준다. 라벨링의 목적은 각 노드의 구조적 역할을 표시하기 위해서이다. 만일 이를 표시해주지 않을 시 GNN에 투입되었을 때 어떤 노드가 target이고 어떤 노드가 얼마나 중요하고(e.g., $1$-hop) 덜 중요한지(e.g., $n$-hop) 알 수가 없는 문제가 생긴다.

라벨링을 결국 해주는 이유는 DGCNN 때문인데, 왜냐하면 DGCNN은 SortPooling을 위해 노드 라벨이 필요하기 때문이다.
라벨링의 정당화에 이어 라벨링 계산 기준에 대해 소개하겠다. 이는 본 연구에서 제안한 Double-Radius Node Labeling(DRNL) 방법이다. 이 해싱 함수는 아래의 기준들에서 유도되었다고 한다.
1) Target 노드 $x,y$는 항상 라벨 1을 갖는다.
2) 노드 $i,j$는 $d(i,x)=d(j,x)\wedge d(j, x)=d(j, y)$를 만족할 때 같은 라벨을 갖는다. 즉 target으로부터 상대적 거리가 완전히 같은 노드들만 같은 라벨을 갖는다.
노드 $i$의 target에 대한 위상적 위치는 radius, 즉 $(d(i,x),d(i,y))$으로 나타낼 수 있다.
결과적으로 두 target 노드 $x,y$와 subgraph에 있는 노드 $i$에 대해 다음과 같은 연산을 거쳐 얻는다.

위 해싱 함수는 완전 해시 함수라고 할 수 있다. 즉 충돌이 절대 일어나지 않는다는 뜻인데 이는 target 노드들에 대해 어떤 위상적 위치에 놓여 있는 노드도 특정적인 라벨을 부여할 수 있다는 것이며 이는 closed-form computation을 가능하게 해준다. 완전 해시 함수에 대한 증명은 다음과 같다.

추가적으로 라벨링 계산에 대해 살펴보자. DRNL은 아래의 특징을 갖는다.

이는 $d(=d_x+d_y)$가 다른 두 노드에 대해 $d$가 큰 노드가 radius도 크며 $d$가 서로 같으면 기하 평균이 큰 노드가 큰 radius를 부여 받음을 표현한다. 이는 이차방식으로 증명이 된다.
또한 $d(i,x)$를 계산할 때 잠시 $y$를 제거한다(역의 경우도 마찬가지). 왜냐하면 이 link를 제거하지 않으면 $i$와 $x$ 사이의 순수한 거리를 측정할 수 없기 때문이다.

라벨링이 끝난 이후 각 노드의 원핫 벡터로 $X$를 구성한다.
2, 3) 노드 임베딩, 노드 특성
앞서서는 구조적인 정보를 라벨링에 넣어주었다. 이제는 노드 자체의 특성을 학습에 포함시켜 줌으로써 모델이 더 풍부한 표현력을 갖추기를 기대한다. 하지만 문제가 있다. 훈련 데이터를 있는 그대로 넣으면 임베딩 자체에 link 관련 정보가 GNN에 의해 빠르게 찾아질 수 있다. 이는 실험적으로 일반화와 성능적으로 좋지 않다고 한다. 이를 해결하기 위해 negative injection을 제시한다. 이 방법은 negative training link(네트워크에는 없지만 negative sample로 사용될 link)를 포함시켜 임베딩 학습을 시키는 것이다.
Latent feature은 네트워크에서 특정 노드의 전역적 영향력, 장거리 영향력을 표현할 수 있다.
Explicit feature은 노드의 자체적 특성이라고 할 수 있다. 예를 들어 소셜 네트워크에서 유저의 프로필 정보처럼 explicit 하게 드러나는 정보들을 의미한다. 이를 학습에 포함시키는 것이 성능 향상에 기여한다고 한다.
전체적으로 보았을 때 3 가지 요소들은 각기 맡고 있는 역할이 다르며(구조적 정보, 네트워크 전체에서의 포지션, 자체 특성) orthogonal 하다고 볼 수 있다.
Experiments
GNN으로 DGCNN과 임베딩 모델로 node2Vec을 사용하였다. 데이터 전체의 link 중 10%는 positive testing, link가 없는 쌍을 negative testing, 나머지 90%와 negative를 통해 training을 구성한다.
실험적으로 $h$가 3이상부터는 성능상 큰 차이가 없다고 한다. 따라서 $h$는 1과 2 중에서 선택한다. 구체적인 선택 기준은 논문을 참고하기를 바란다.
Metric은 AUC(ROC 곡선의 밑넓이)와 AP(Average Precision)를 사용한다.

위는 휴리스틱들을 사용하는 모델들과의 비교이다. 이들은 노드 특성들을 사용하지 않기 때문에 SEAL도 노드 특성들에 접근하지 못하게 모델을 제한한다.
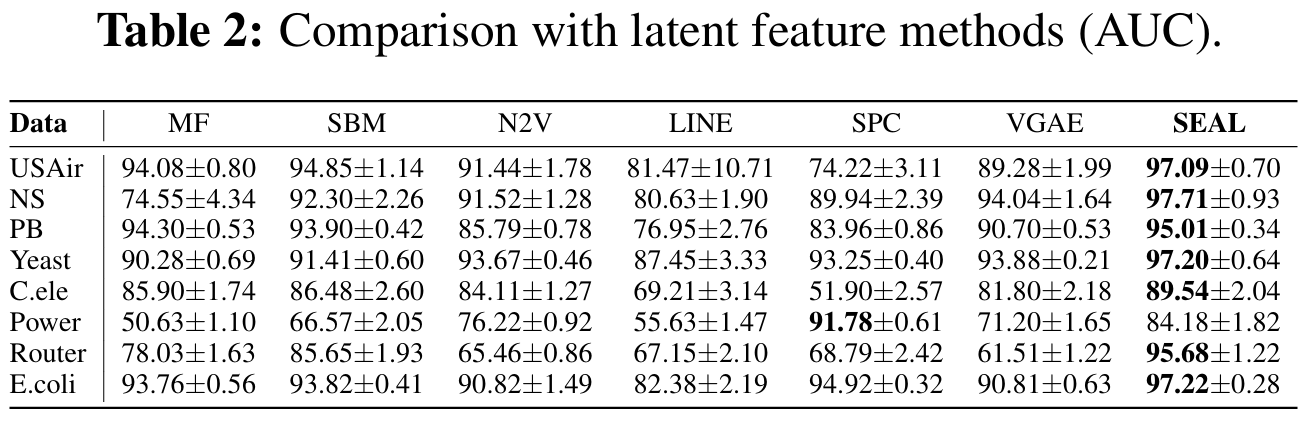
위는 latent feature들을 사용하는 모델들과의 비교이다. 하지만 explicit 정보는 사용하지 않으므로 SEAL의 $X$에서 explicit feature를 제외한다.

SEAL에 explicit feature를 포함시킨 결과이다. Explicit feature는 모든 데이터에서 얻을 수 있는 것이 아니기 때문에 제한된 데이터에 대해서만 평가가 가능하다.
Conclusion
휴리스틱을 pre-defined 했던 기존의 여러 접근법들과는 다르게 네트워크가 주어지면 그 네트워크에 가장 잘 맞는 휴리스틱을 GNN으로 학습할 수 있는 모델을 만들었다. 이를 통해 어떤 특징을 가지는 네트워크가 주어져도 link prediction이 가능한 범용성을 얻을 수 있다. 또한 그래프의 구조뿐만 아니라 latent, explicit feature를 포함시켜 더 풍부한 표현을 학습할 수 있게 기반을 다졌다.