Presentation pptx 자료
문제:
앞서 GNN, GCN, GraphSAGE 등 그래프 구조에 Neural Network를 적용하려는 시도가 다수 있었다. NN 사용이 그래프에서 더 힘든 이유는 개체(노드)들의 연관성이 일반 그리드와 같은 선형적인 구조에 비해 복잡하기 때문이다. 그래서 이와 같은 복잡성을 타개하기 위해 여러 노력이 있었지만 그 연구들은 모두 노드 간의 엣지를 모두 같은 가중치로 생각해 주었다. 즉 기존에는 "연결되어 있다", "연결이 안 되어 있다"만 관찰했다면 GAT에서는 "얼마나 강하게 연결되어 있는가?"도 계산의 대상에 포함한다는 점에서 기존의 연구들과 차별점이 있다.
필요성:
여태까지 우리는 노드의 피쳐와 다른 노드와의 연결 유무만을 주관심사로 두었다. 하지만 본 논문에서 재기한 문제는 에지들 간의 연결정도가 존재할 거라는 것이다. 같은 이웃이라고 해서 같게 취급하지 말자는 뜻이다. 예를 들어 소셜 네트워크에서 어떤 인물 A를 주변으로 다수의 사람들을 이어주는 다수의 엣지들이 있을 것이다. A는 이웃들과 동등하게 친할 것이라는 보장이 없기 때문에 attention이 그래프에서 유용하게 사용될 수 있는 이유이다. 즉 attention(집중)은 나 자신(노드)을 임베딩 하기 위해서 이웃에 얼마나 "집중" 해야 하는지 결정해 주는 척도이다.
Architecture
먼저 우리가 입력층에서 사용할 노드들을 다음과 같이 표현한다.
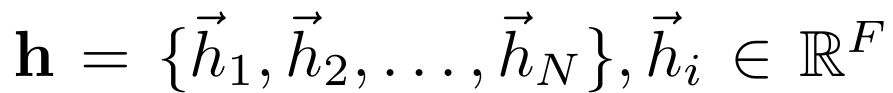
$\vec{h_i}$ : $i$번째 노드 벡터
$N$ : 노드의 개수
$F$ : 1개의 노드에 있는 피쳐의 개수
즉 노드들의 집합이라고 볼 수 있다.
이제 우리의 목적인 노드 임베딩 결과는 출력층에서 다음과 같을 것이다.
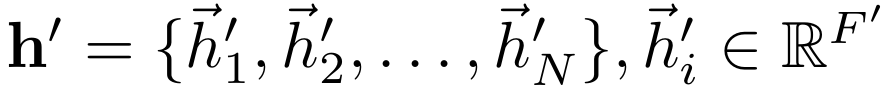
$\vec{h_i^{'}}$ : $i$번째 노드의 임베딩 된 벡터
$F'$ : 임베딩 차원
$F$차원에서 $F'$차원으로 벡터를 변환하려면 선형 변환을 위한 행렬이 필요하다. 따라서 weight matrix가 필요하다.

즉 단순히 노드가 임베딩 되는 방법을 생각해 보면 아래와 같다.$\mathbf{W}\vec{h_i}=\vec{h_i^{'}}$
여기서 살을 덛붙여 attention을 임베딩 과정에 추가해 주는 것이 GAT의 전부이다. Attention을 결정하는 attention coefficient는 다음과 같이 정의된다.
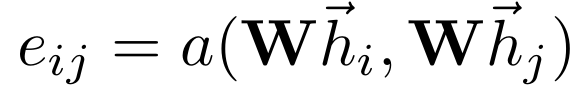
$a$ : attention coefficient를 계산해 주는 함수. 결괏값은 실수이다($\mathbb{R}^{F'}\times \mathbb{R}^{F'}\to \mathbb{R}$)
$e_{ij}$ : 노드 $i$에 대해 노드 $j$가 얼마나 중요한지 나타내는 attention coefficient
하지만 막무가내로 모든 두 노드들에 대해 attention을 계산해 주면 모든 노드끼리 연결성을 부여하는 대신 그래프의 구조적 정보를 잃게 된다.
→ In its most general formulation, the model allows every node to attend on every other node, dropping all structural information.
그래서 노드 $i$를 기준으로 그 주변 1 hop 거리의 이웃들과의 attention만을 계산한다. 이를 mask attention이라고 한다.
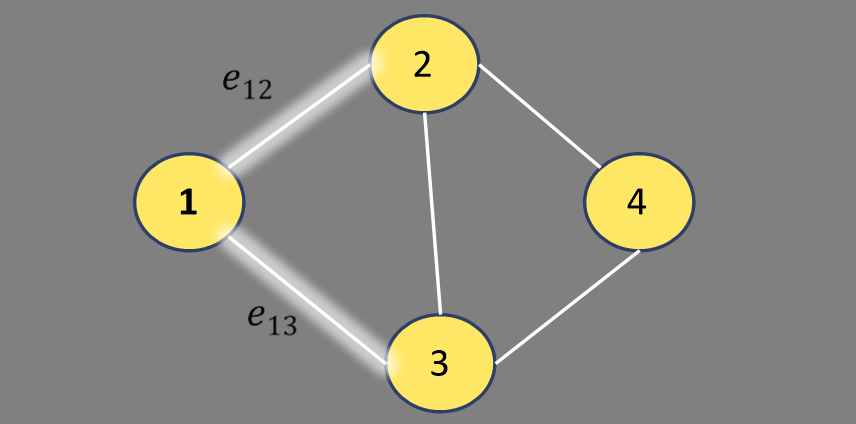
1번 노드 기준으로 이웃은 2와 3 뿐이므로 attention을 2개만 계산해 주면 된다.
추가적으로 해주어야 하는 작업이 있는데, 그것은 바로 특정 노드로부터 계산된 모든 attention을 softmax로 normalize해주는 것이다. Normalization이 굳이 필요한 이유는 무엇일까? Softmax를 적용하지 않은 경우와 적용한 경우를 비교해 보자.

구조 1과 구조 2는 서로 독립적인 그래프 구조이고 attention은 구조 1의 경우 2, 5, 1과 구조 2의 경우 10, 10, 10으로 계산되었다. 1번과 3번 노드의 attention을 보았을 때 직접 비교를 해보면 구조 2에서 두 노드 간의 연결성이 강함을 알 수 있지만 우리가 attention으로 알고 싶은 정보는 이웃 노드들 간의 상대적인 집중도이기 때문에 우측의 normalization 이후의 attention이 더 신뢰성 있는 정보이다. 또한 이후에 연산 크기가 너무 커지는 것을 방지해 준다.
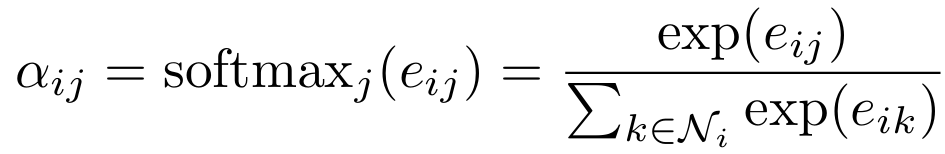
이제 $a$함수를 정의해 보자.
두 임베딩된 노드를 이어 붙인 다음 이렇게 생성된 벡터를 single-layer feedforward NN으로 통과시킨다.

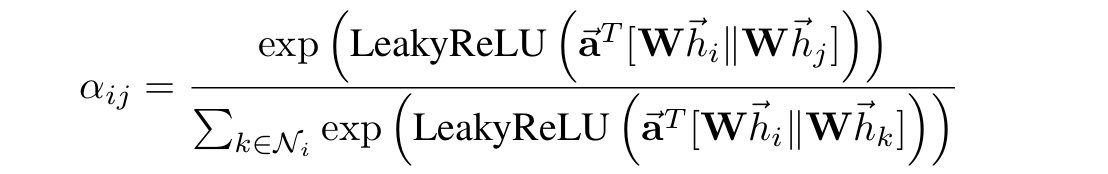
$\left| \right|$는 두 벡터를 위아래로 이어 붙이겠다(concatenate)는 뜻이고 $\vec{\textbf{a}}$는 업데이트가 가능한 파라미터 행렬이다. 이후 계산 결과를 ReLU의 문제점을 보완한 LeakyReLU를 활성화 함수로 통과시켜 준다.
여기까지가 attention coefficient를 계산하는 방법이다.
이제 우리의 본래 목적이었던 노드 임베딩 과정을 알아보자.

위의 수식을 해석하자면 다음과 같다 "i노드의 1 hop거리 이웃에 대해서 각각 attention을 계산해서 곱해주고 weight matrix(W)를 곱해준 뒤 그 결과를 모두 합한 후 활성화 함수로 통과시켜 준다."
하지만 여전히 위의 연산과정을 안정화하기 위한 방법이 필요하다. 그래서 averaging을 이용한다.
이 방법은 multi-head attention이라고도 불리는데 방법은 다음과 같다.
독립적인 K개의 mechanism(파라미터들, $W$, $\vec{\textbf{a}}$)을 따로 실행시켜 그 결과를 마지막에 평균내서 최종 업데이트를 진행한다.
이 multi-head attention을 통해서 얻을 수 있는 장점들은 첫 째, 각 mechanism마다 습득하는 특성들이 존재할 것이기 때문에 그래프의 다양성을 포착할 수 있다. 둘째, 여러 연산 값을 평균내기 때문에 훈련도중 더 안정적인 gradient를 습득할 수 있다.
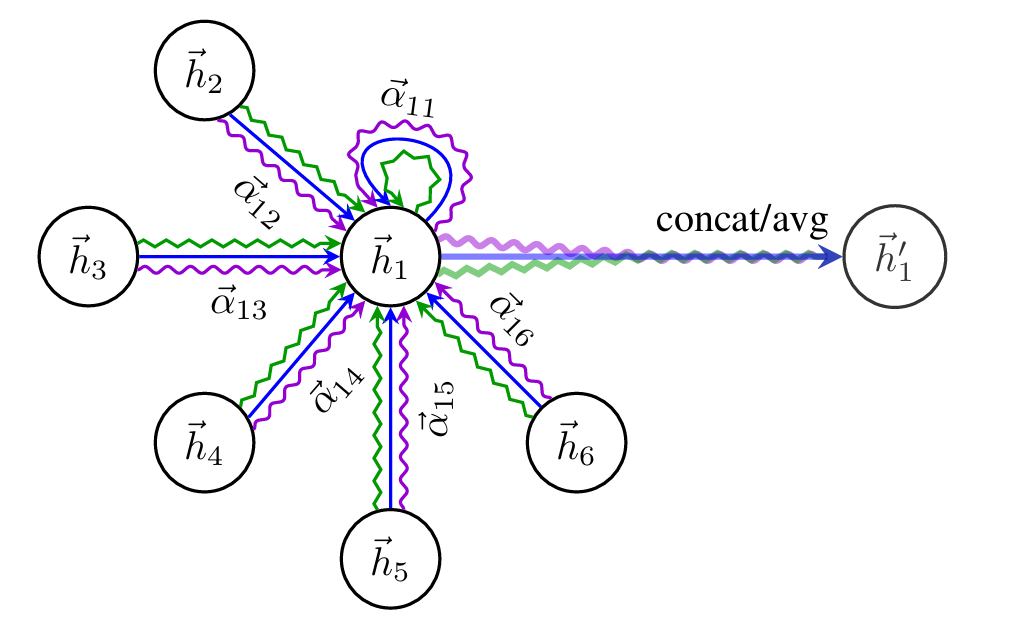
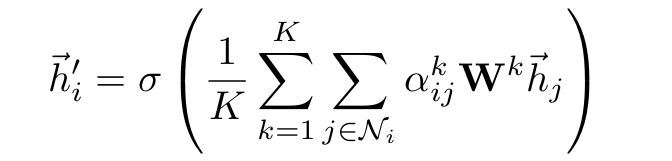
여기서 위로 첨자가 되어 있는 $k$는 $k$번째 mechanism의 attention($\alpha$), weight matrix(\textbf {W})를 의미한다. 즉 같은 $k$값을 갖고 있지 않으면 서로 무관한 상태에 있는 변수들이다(물론 averaging 이후 backpropagation을 통해 어느 정도 영향을 받겠지만 forward passing에서는 서로 독립적인 것은 사실이다).
Comparisons to realated work
GAT는 과거의 모델들에 비해 이점이 많은 모델이다.
1. 컴퓨팅적으로 효율적이다.
시간복잡도는 다음과 같다.

선형 결합 과정(Wh) : $O(|V|FF')$
두 엣지간의 attention 계산 : $O(|E|F')$
normalization(softmax) : $O(|E|)$
feature aggregation : $O(|E|F')$
sigmoid : $O(|V|F')$
2. 엣지에 다른 가중치를 부여해준다.
3. Transductive 뿐만 아니라 inductive learning에도 적용 가능.
GCN의 경우 그래프의 라플라시안을 미리 계산해주었지만 GAT에서는 그런 연산은 불필요하다. 주변 이웃들의 정보에만 의존하기 때문에 그래프의 구조적 특성에 모델의 성능이 상대적으로 독립적이다.
4. 고정된 크기의 이웃을 sample하지 않아도 된다.
GraphSAGE는 sampling하는 이웃의 갯수를 일정하게 제한하였지만 이는 그래프의 순수 구조를 무시하는 것이기 때문에 추론 과정에 방해가 된다.
'Graph Networks > Graph embedding' 카테고리의 다른 글
| Inductive Representation Learning on Large Graphs(GraphSAGE) 리뷰 (3) | 2024.07.11 |
|---|---|
| [GCN] Graph Convolutional Networks 논문 리뷰 (1) | 2024.06.07 |
| node2vec : Scalable Feature Learning for Networks 리뷰 (1) | 2024.05.31 |


