Paper :
Presentation pptx 자료
주요 관심사
우리의 현실에 노드로 대변될만한 개체들을 상상해 보자. 가장 단순한 예시는 '사람'일 것이다. 그렇다면 이제 그 사람을 나타내기 위한 속성들이 무엇이 있을지 상상해 보자. 당장 생각나는 것만 해도 나이, 직업, 인종, 출신지, 출신국가, 거주지, 가족 관계등 매우 많다.
즉 우리는 하나의 고차원 노드이다. 또한 우리는 다른 노드(사람)들과 연결하여 복잡한 그래프를 이루게 된다. 이 복잡한 그래프에서 연구자들이 수행하기를 원하는 task는 크게 다음 3 가지이다.
1. classification
2. link prediction
3. clustering
물론 위와 같은 task말고도 무궁무진하게 많은 문제 상황에 적용할 수 있지만 크게 3 가지를 수행하고자 모델을 만든다. 이를 실현하려면 가장 먼저 선행되어야 하는 것이 노드 임베딩이다. 임베딩은 고차원의 데이터를 그 특성을 잃어버리지 않으면서 저차원의 데이터로 변환하는 것을 말한다. 그냥 노드 그 자체에서 만족할 수는 없을까?
High-dimensional space에서는 task를 수행하기 쉽지 않다. 왜냐하면 차원의 저주성(curse of dimensionality) 때문인데, 이는 sparse한 벡터 간의 비교 결과가 의미가 없다는 뜻이다. 따라서 비교 작업을 위해 sparse 벡터를 dense 벡터로 변환해 주는 작업이 필요하다.
문제점
Node embedding을 위해 다양한 모델들이 제시되었다. node2Vec, DeepWalk, GCN 등이 제시되었다. 하지만 필자가 지적하는 것은 기존의 모델들은 transductive learning(반지도 학습)에서만 좋은 성능을 보여준 데에 있었다.
Transductive learning이 어떻게 동작하는지 알면 단점을 알 수 있다. Training data와 testing data를 모두 학습에 이용하고 이 과정에서 testing data에 대한 임베딩 작업을 수행한다. 즉 testing data(unseen data)에 대한 임베딩을 하고 싶으면 전체 데이터가 매번 필요하다.
즉 새로운 노드의 출현에 취약하다. 파라미터 재탕(?)을 못하기 때문이다.

생각해보면 현실 세계에서는 정보의 추가와 삭제가 빈번히 일어나기 때문에 transductive learning에 특화된 모델은 현실적으로 사용하기 어려운 것을 알 수 있다.
해결
이 노드 임베딩 문제를 inductive learning 문제로 끌고 오는 것이 GraphSAGE의 독특함이다. 필자는 결국 더 general 한 모델을 만들고 싶었던 것이다. GraphSAGE는 검증을 통해 inductive learning뿐만 아니라 transductive learning에서도 우수한 성능을 보여줌이 입증된다.
GraphSAGE 구조
Inductive learning 문제로 끌고 오기 위해서 SAGE는 어떤 전략을 취할까? 아래는 본 SAGE의 전반적인 방법론에 대해 설명해준다.

아직 무슨 뜻인지는 모르겠지만 1번부터 차근차근 따라가 보자.
1. Sample neighborhood
노드 1개를 임베딩하는 작업에 초점을 맞춰보자. 노드 1개를 임베딩하기 위해서는 그 노드를 나타내는 특징들이 필요하다. 따라서 현 모델에서는 가정을 내린다. "이웃 노드들은 유사하다". 이 가정에 의해 목적 노드를 기준으로 K hop거리의 노드들을 sampling 할 것이다. Sampling 전략은 크게 2가지로 나뉜다, 그래프 전체를 sampling 하거나 일부만 sampling(minibatch approach)할 것이다. 이에 대한 논의는 다음 aggregation에서 이루어진다.
2. Aggregate feature information from neighbors
알고리즘을 살펴보기 전에 기호들에 대해 알고 넘어가자.

$K$는 샘플링할 노드 hop의 거리이다. $K =3$ 이면 임베딩을 위한 기준 노드로부터 3 hop만큼의 이웃들까지만 모은다는 뜻이다.AGGREGATEk는 샘플링된 노드들을 요리(?)할 함수이다(aggregate의 사전적 의미는 합계, 종합이 있다). 즉 k hop에서 모아진 노드들을 조합해서 새로운 특징 벡터로 변환하는 작업을 수행하는 함수이다. 이 함수에 정확한 동작은 논문의 가장 마지막에 소개된다. 지금은 그냥 노드 믹서기 정도로만 이해해 두자.

k hop에서 사용될 가중치 행렬이다. 즉 $K = 3$ 일 때 1 hop거리에서 사용할 weight와 3 hop거리에서 사용할 weight가 다르다는 뜻이다.
먼저 이웃 전체를 사용하는 알고리즘을 살펴보자(그래프 전체를 학습시킨다).

1 hop 에서부터 Bottom-Up 방식으로 K hop까지 단계를 밟아간다. 3번째 줄에 보면 전체 그래프를 학습시킨다. 노드 v의 주변 이웃을 aggregate 한다. 단, 이때 aggregate 되는 벡터는 이전 hop에서 완성된 임베딩 노드이다. Aggregate 된 결과 노드와 (k-1) hop 임베딩 v를 이어 붙여(concatenation) W와 곱해주어 k hop에서의 임베딩을 얻는다. 이것(k hop거리의 이웃까지 사용한 임베딩)이 모두 완료되면 normalize 시켜주고 K hop 이후에는 z로 새로운 최종 임베딩을 명명하며 K hop 임베딩을 완료시킨다.
하지만 이 알고리즘의 문제점은 각 hop에 대한 계산을 할 때 그래프 전체가 필요한 점이다.
계산의 방대함을 막기 위해 minibatch sampling 전략을 채택한 새로운 알고리즘이 있다.

배치 BK부터 B0까지 수집한다. 눈에 띄는 부분은 Top-Down 방식으로 노드를 수집한다(hop의 수가 적을수록 노드가 많아진다). 왜 이런 방식을 취할까? 반대로 B0로 시작해서 BK으로 오름차순으로 샘플링한다고 생각해 보자. 만약 B0의 크기가 어느 수준으로 크고 K의 값이 크면 결국 BK는 전체 그래프의 크기에 도달할 것이다. 왜냐하면 주변 이웃들을 샘플링하다 보면 집합의 크기는 계속 커지기 마련이다.
또한 차라리 B0의 크기가 큰 것이 작은 것보다 낫기 때문이다.
본 논문에서는 이 알고리즘을 더 선호하는 것으로 보이고 K=2일 때 최적이라고 주장한다.
그리고 시간 복잡도의 일정성을 위해 fixed size of neighborhood를 샘플링한다.
3. Predict graph context and label using aggregated information
앞에서 샘플링과 임베딩을 살펴보았고 이제 loss function과 aggregate 함수의 형태를 살펴보자.
Loss function
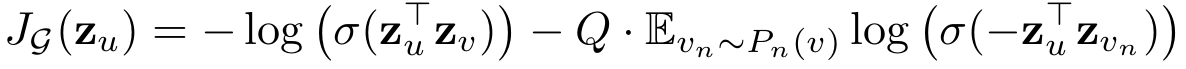
임베딩된 노드들로 구성되어 있음을 알 수 있다. 전체적인 구조상 u 노드와 v노드를 가까이,
vn노드를 멀리 학습시키려는 것을 알 수 있다. vn은 negative sampling 된 Pn(v)으로부터 추출된 노드이다. Q는 Pn(v)의 크기이다.

이 부분을 이해할 때 주의해야 하는데, Q를 제외한 부분이 한 덩어리이다. 즉 Pn(v)에 샘플링된 모든 노드로 계산한 log값을 평균내고 negative sampling 된 크기만큼의 파급력을 전달해야 하기 때문에 마지막에 Q를 곱해준다.
위의 손실 함수는 unsupervised에 사용되고 supervised learning에 대해서는 cross entropy 같이 자유롭게 사용해도 된다고 한다.
Aggregation function
본 논문에서는 3개의 함수를 제안한다.
● Mean aggregator

중심 노드를 기준으로 본인 포함 1 hop거리의 이웃들을 모아서 모든 feature에 거쳐 평균을 내고 single layer NN에 통과시켜 준다.
필자는 이 함수가 GCN과 흡사한 함수라고 한다. 검증 부분에서 한 번 더 언급될 예정이다.
● LSTM aggregator
LSTM 구조에 기초한 함수이다. 하지만 permutation invariant 하지 못해 1 hop 이웃에 관해 random 하게 뽑아 input으로 넣어준다. 구체적인 수식은 공개되어 있지 않다.
● Pooling aggregator

이웃노드를 bias가 있는 single layer NN에 통과시키고 그중에서 최댓값을 취한다. 경험적인 실험 결과에 의하면 필자는 max-Pooling과 mean-Pooling의 성능적인 차이가 별로 없다고 덧붙였다.
검증

F1 score을 통일적으로 사용했다. GraphSAGE-GCN은 GraphSAGE의 알고리즘 1에서 4, 5번째 줄을 조금 수정한 mean aggregator를 이용하는 알고리즘이다. 이를 통해 GraphSAGE는 supervised, unsupervised 모두에서 잘 동작하는 모델임이 증명되었다.
'Graph Networks > Graph embedding' 카테고리의 다른 글
| Graph Attention Networks 리뷰 (0) | 2024.07.05 |
|---|---|
| [GCN] Graph Convolutional Networks 논문 리뷰 (1) | 2024.06.07 |
| node2vec : Scalable Feature Learning for Networks 리뷰 (1) | 2024.05.31 |


