Paper :
Main interest
문제는 지식 그래프(Knowledge Graph, KG)의 생성으로 거슬러 올라간다. 본 연구에서 소개하기로 NELL(Never-Ending Language Learner)은 실시간으로 다량의 웹 데이터를 입력받아 텍스트에서 정보를 추출해 기존에 쌓아두었던 KB(Knowledge Base, KB)를 업데이트한다. 문제는 우리가 이 세상에 있는 모든 데이터를 끌어모을 수 없다는 한계 때문에 NELL을 통해 구축된 KB는 imperfect 하다. 이 문제를 해결하기 위해 KB에서 추론을 할 수 있는 모델을 만들자는 움직임이다. 즉 imperfect 한 것은 어쩔 수 없으니 빈 공간을 모델이 채우게끔 시키자는 것이다. 이는 NELL이 생성하는 KB뿐만 아니라 추천 시스템, 자연어 처리 등에서도 범용적으로 사용할 수 있다.

하지만 본 연구에서는 NELL의 KB에서 추론을 할 수 있는 모델 구축에 집중한다.
먼저 NELL이 데이터를 생성하는 방법에 대해 간략하게 소개하겠다. NELL은 2010년부터 시작된 프로젝트이며 24시간 웹을 읽는 능력을 꾸준히 향상시키고 있으며 NELL이 추출한 정보들은 신뢰도 높은 belief와 비교적 신뢰도가 낮은 candidate belief로 나뉜다.
NELL은 입력으로 다량의 웹과 ontology를 받는다. 여기서 ontology란 category(주로 명사형의 노드가 될 수 있는 대상의 집합, e.g., person, athlete, sports)와 배우고자 하는 관계(e.g., athletePlaysSprot(<athlete>, <sport>))를 뜻한다. 즉 웹으로부터 ontology에서 요구하는 관계(relation)를 학습하고자 한다. 예를 들어 아래와 같이 정보를 추출해 KB를 채우는 방식을 기대한다는 것이다.
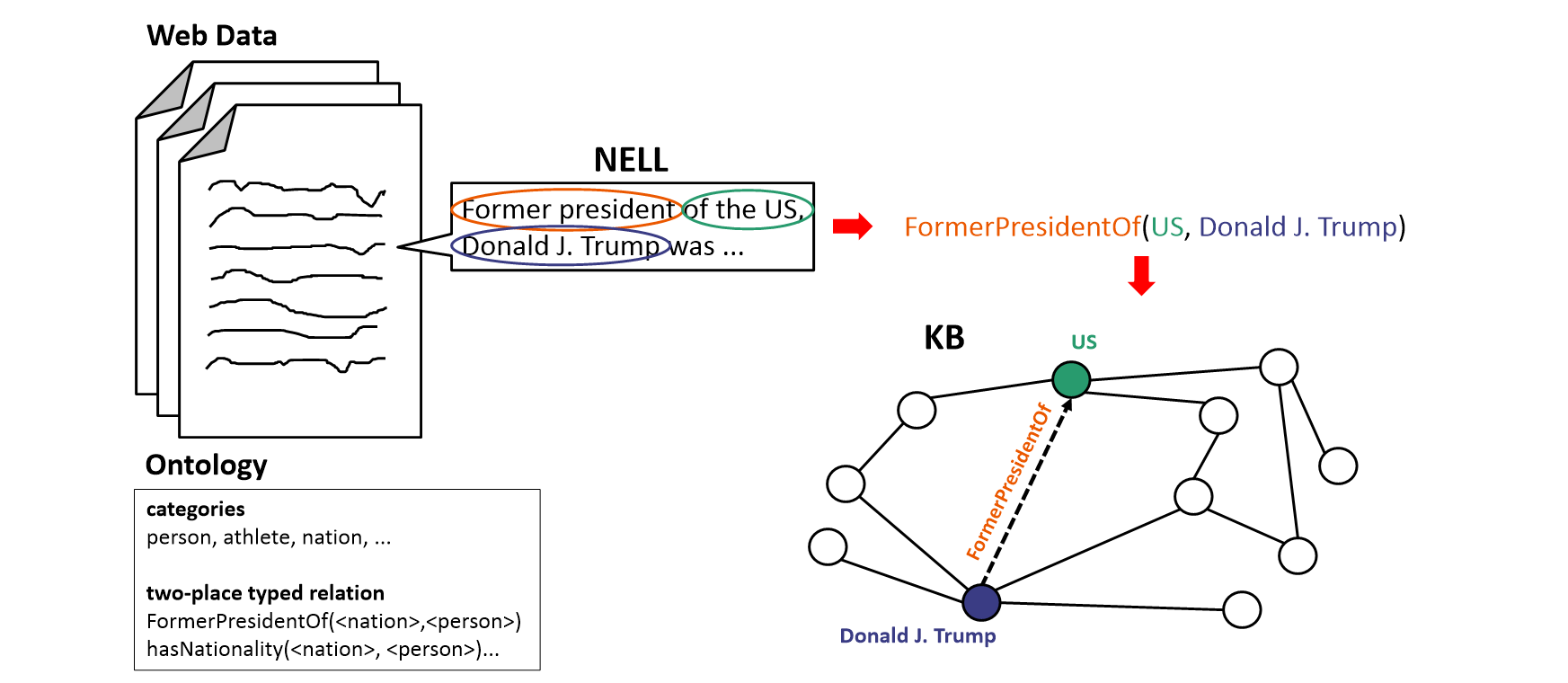
NELL의 구체적인 작동 방법을 전부 알 필요는 없다. 단, 두 가지 정도면 언급하고 넘어갈 가치가 있다.
첫째, NELL은 다전략 학습 시스템이다. 1500개 이상의 분류, 추출 기법을 보유하고 있는 반지도 학습 모델이며 데이터로부터 서로 다른 측면에서 집중하는 시스템들로 이루어져 있다.
둘째, 학습한 결과들로 재 학습을 하기 때문에 bootstrapping system이다.
Problem with previous models
NELL을 통해 거대한 크기의 KB를 구축할 수 있게 되었지만 추론을 수행하는 능력에는 여전히 한계가 있었다. 당시에 NELL이 갖고 있던 유일한 추론 기법은 일차 Horn clause rules를 활용해 갖고 있는 belief들로부터 새로운 belief를 생성하는 것이다.

이렇게 추출된 rule은 조건부 확률(신뢰도)을 가진다(전제가 참일 때 결론도 참일 확률).
NELL은 FOIL 알고리즘의 변형, N-FOIL을 이용해 rule들을 학습한다. 이는 positive, negative example을 동시에 입력받아 Horn clause가 많은 positive와 적은 negative를 추론하는 방향으로 학습이 진행되며 "separate-and-conquer" 전략을 사용해 학습한 Horn clause들이 data에 fit 되기를 바란다. 구체적으로는 general 한 rule에서 시작해 점차 specialize 하여 Horn clause를 학습한다. 이 과정에서 clause가 학습되면 clause가 성공적으로 추론한 example은(separate) training set에서 제거되고 positive example이 더 이상 남아있지 않을 때까지 이 과정을 반복한다(conquer).

하지만 이 방법은 positive, negative example을 구하기 위해 넓은 search space를 요구하며 어떤 Horn clause는 평가하기 비쌀 수 있다. 따라서 N-FOIL은 두 가지 가정을 한다.
첫째, consequent predicate는 일대일 대응이다(functional). 즉 어떤 positive example에 대해 $a$가 정해져 있으면 $c$는 유일하다는 것이다. 이 가정을 통해 negative example을 쉽게 얻을 수 있게 된다.
둘째, "relational pathfinding"으로 general rule을 생성한다. 즉 consequent를 정하고 $a$에서 시작해서 $c$로 끝날 수 있는 경로(preconditions)를 general rule로 뽑는다.
이렇게 추출된 rule들은 Dirichlet prior로 신뢰도가 계산된다.
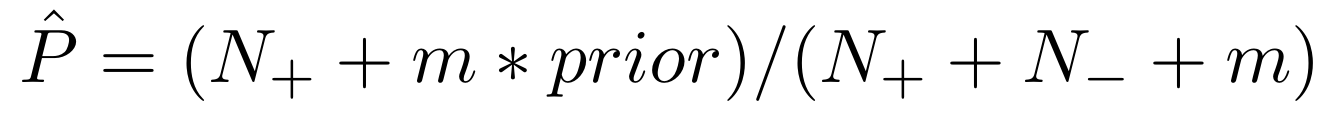
$N_+$는 rule을 만족하는 positive example의 개수이고 $N_-$는 rule을 만족하는 negative example의 개수이다. $m=5, prior=0.5$로 설정된다.
사실 우리한테 중요한 것은 이것이 아니다. 본 연구의 진정한 contribution은 N-FOIL의 방식보다는 2010년에 본 연구의 연구자들이 개발한 Path Ranking Algorithm(PRA)을 여기에 활용한 것이다. 즉 random walk를 사용해 Horn clause inference보다 더 향상된 성능을 보여준다.
Architecture
Path Ranking Algorithm(PRA) Peview
PRA는 쿼리 노드 $a$가 주어졌을 때 노드 $b$를 rank 하는 방법을 학습한다.
PRA는 먼저 고정된 크기의 path type를 수집한다. N-FOIL에서 clause를 모았던 것과 마찬가지로 말이다. 이때 path type는 ranking "전문가"라고 부를 수 있다. 즉 "전문가"의 edge type(relation) 순서대로만 쿼리 노드에서부터 이동하여 그들이 갖고 있는 weight로 노드들을 rank 한다. 마지막으로 여러 전문가들로부터 얻은 weight들을 통합해 로지스틱 회귀로 $R(a, b)$가 참일 확률을 구한다.
Random walk는 현재 walk가 위치해 있는 노드에서 간선의 개수에 따라 이동 확률이 달라진다. 아래와 같은 예시를 들 수 있다.
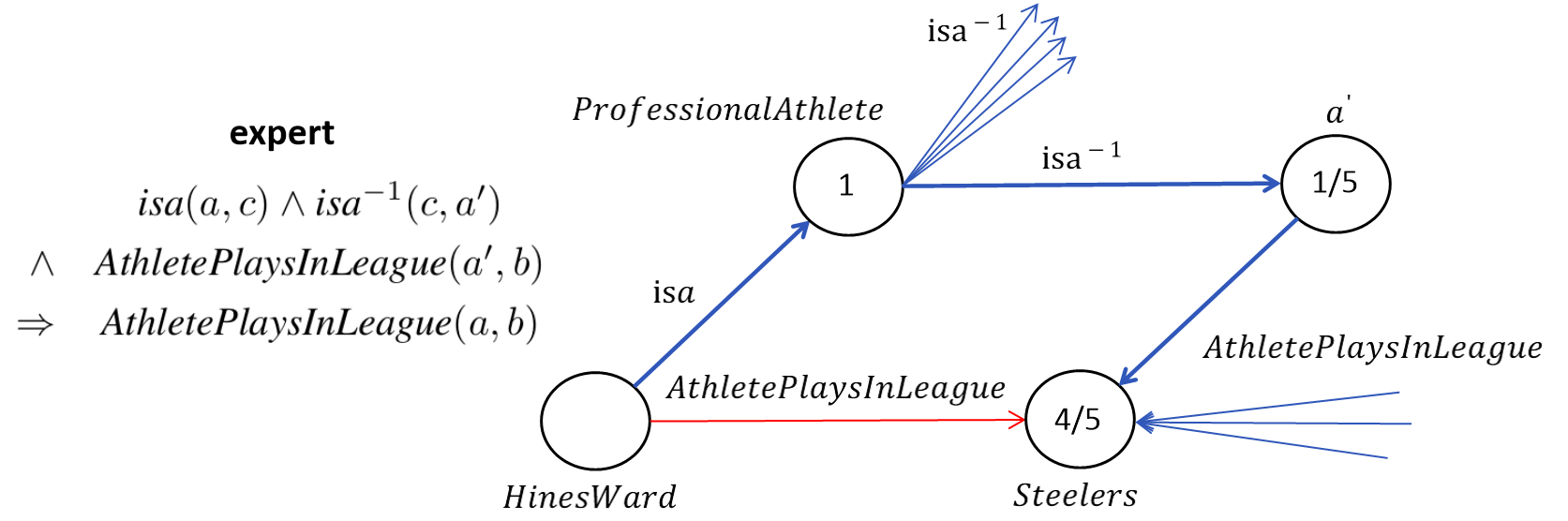
위의 예시로만 봤을 때 "전문가"가 담당한 rule은 높은 precision을 갖고 있지는 않지만 random walk를 통해 주어진 KB에서 경로들을 탐색해 높은 품질의 rule을 도출할 수 있다는 것을 보여준다. 이와 같은 알고리즘을 Path Based라고 부르는 이유이다. 물론 이 특성들은 KB가 진화함에 따라 walk의 확률이 달라짐에 기인하여 달라질 수 있다.
N-FOIL과 함께 생각해 봤을 때 PRA의 특징은 아래와 같다.
1. Predicate이 functional 하다는 가정이 필요 없다.
2. Relation instance $R(a, b)$에 대한 support 점수는 여러 path들의 통합으로 계산된다.
3. 추론의 신뢰도는 KB의 상태와 쿼리 되는 entity에(본 논문의 "Giants" 예시 참조) 따라 민감하다.
이제 구체적으로 PRA의 학습 방법에 대해 알아보자. 참고로 PRA가 처음 소개된 것은 2010년이고 본 연구는 2011년에 기존 PRA에 몇 기능들을 추가해 출판되었다.
$P$는 연속된 relation path로 정의되어 있다. 즉 precondition들이 이에 해당한다.

이후에 experiment에서 entity 대신 concept로 대체해 표현한다. 이를 통해 학습된 rule은 entity independent 하다는 것을 알 수 있다.
어떤 경로를 학습할 것인지에 대해서는 후반부 "Data-Driven Path Finding"에서 더 자세히 다루겠다.
경로 $P$에 대해 시드 노드 $s\in domain(P)$에 대해 '제한된 경로의 random walk'로 분포 $h_{s, P}$를 정의할 수 있다. $P$가 비어 있는 경우, 비어 있지 않은 경우에 대해 아래와 같이 각각 정의할 수 있다. 단, 비어 있지 않은 경로를 $P=R_1,..., R_l$이라고 한다면 $P'=R_1,..., R_{l-1}$로 정의한다.
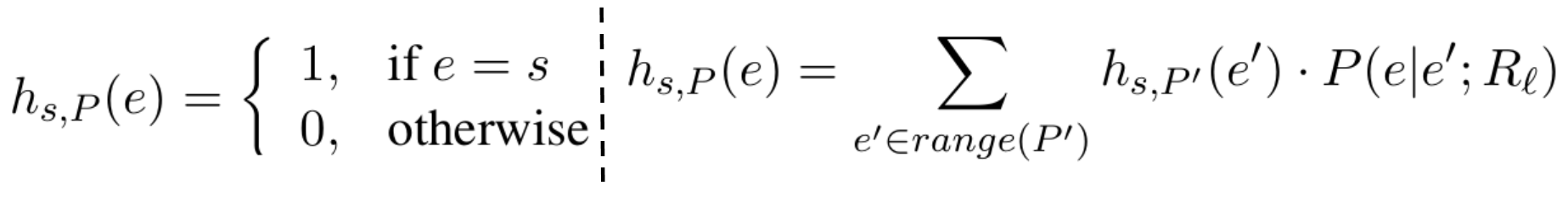
여기서 $P(e|e';R_l)$은 $R_l(e', e)/|R_l(e',\cdot)|$로 정의된다. 즉 경로가 비어있지 않은 경우에 대해서 ($e'$에 도착할 확률)$\times$($R_l(e', e)=1$인 경로에 대한 random walk 확률값)의 총합으로 결정된다. 참고로 $a\overset {R}{\rightarrow }b$를 만족하면 $R(a,b)=1$, 아닐 시에는 $0$이라고 할 수 있다.
이제 경로가 주어졌을 때 시드 노드에서 종점 노드까지 도달할 확률을 계산할 수 있게 되었다. 여기서 일반적인 상황으로 확장해서 주어진 경로 집합 $P_1,...,P_n$이 있다면 그에 각각 대응되는 $h_{s,P_i}(e)$는 path feature라고 할 수 있다. 즉 아래와 같이 최종적으로 쿼리 노드 $s$에서 출발해 어떤 노드 $e$에 도달할 확률은 다음과 같이 나타낼 수 있다.

즉 위의 수식을 활용하여 relation $R$과 $R(s_i,t_i)$의 값을 알고 있는 노드 쌍 집합 $\left\{ (s_i,t_i) \right\}$를 이용하면 훈련 데이터 $\textbf{D}=\left\{ (\textbf{x}_i,y_i) \right\}$를 구성할 수 있다. 여기서 $\textbf{x}_i$는 $(s_i,t_i)$에 해당하는 path feature들을 모아 놓은 벡터이고 $y_i$는 $R(s_i,t_i)$가 참인지에 대한 불리안 값이다. 그림으로 표현하면 아래와 같을 것이다.
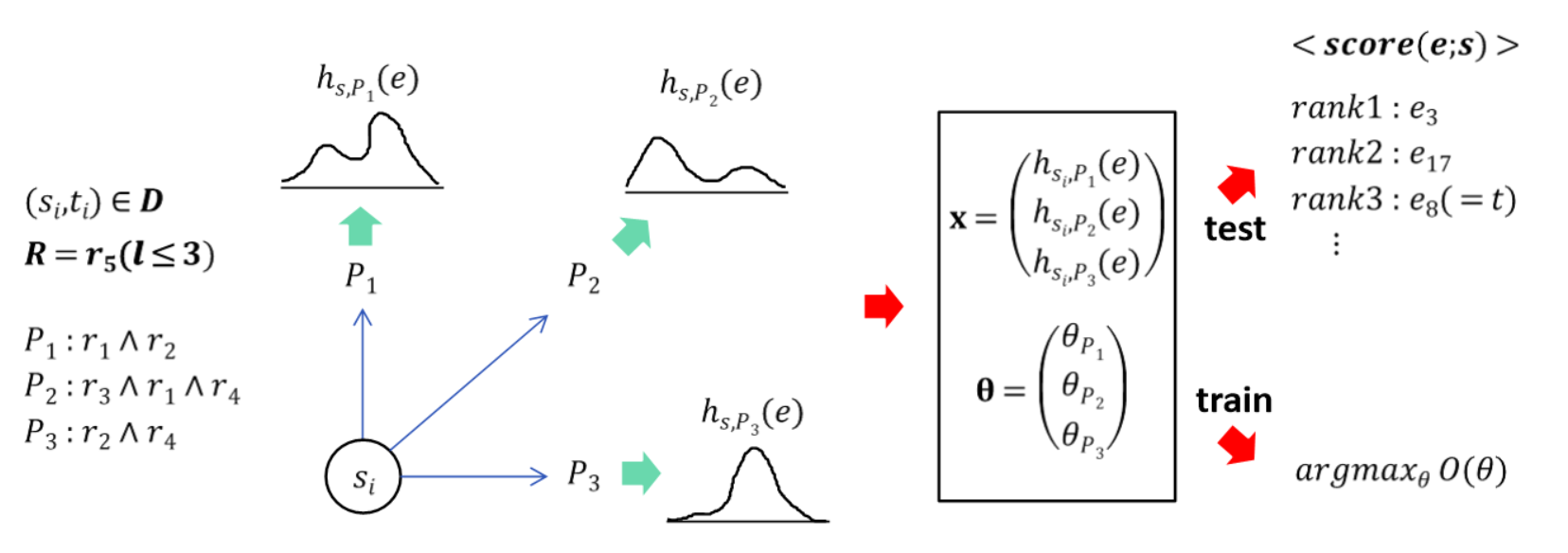
학습될 파라미터들은 $P(y|\textbf{x};\theta)$를 정확히 예측하는 방향으로 로지스틱 회귀로 학습되며 목적 함수는 아래와 같다.

$\lambda _1,\lambda_2$는 각각 L1 정규화, L2 정규화 조절 파라미터이고 $o_i(\theta)$는 아래와 같다.
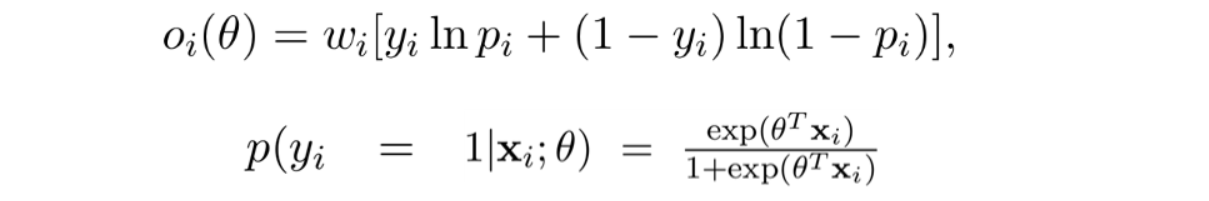
훈련 과정에서 2010년에 제시된 PRA에서 제안한 biased sampling으로 negative sampling을 사용한다.
Data-Driven Path Finding
KB에서 조합 가능한 모든 길이 $l$이하의 경로에 대해 학습하면 이상적이겠지만 이때 경로의 개수가 기하적으로 급증하기($|R|^l$) 때문에 현실적이지 않다. 따라서 본 연구에서 제시된 PRA에서는 학습 가치가 있는 경로를 아래와 같이 정의한다.
1. 쿼리 노드 $s$가 경로 $P$를 $h_{s,P}(e)$만큼 support 한다고 정의하자. 이때 $P$에 의해 훑고 지나가지는 모든 노드 $e$에 대해 $h_{s,P}(e)$의 값이 $\alpha$보다 커야 한다. 실험에서 $\alpha$는 0.01로 세팅했다.
2. 경로 $P$는 쿼리 노드 $s$에서 시작해서 target 노드 $t$에 실제로 도착해야 한다. 물론 이때 $R(s,t)=1$이어야 한다. 즉 실제로 닫히는 경로만 학습 가치가 있다고 가정한다는 것이다.
추가로 L1 정규화로 경로의 개수를 더 줄일 수 있다고 하는데, 맥락상 경로에 해당하는 파라미터 값이 너무 작아지면 그 경로를 버린다는 뜻으로 해석된다.
위의 조건들을 토대로 아래의 Table 1을 보면 search space를 효과적으로 줄일 수 있다.

모델 자체에 대한 설명은 전부 끝났다. 이제 마지막으로 샘플링 증진 부분만 남았다.
Low-Variance Sampling(LVS)
기존의 PRA에서는 finger printing, particle filtering으로 random walk의 속도를 향상할 수 있었다고 한다. 하지만 이는 노드 선택에 있어 다양성을 훼손한다고 한다. 예를 들어 나가는 간선이 2개인 노드에 walker 2개가 도착했을 때 50%의 확률로 두 walker 모두 하나의 간선만 탄다는 것이다.
이를 해결하기 위해 LVS를 사용해 샘플링을 한다.
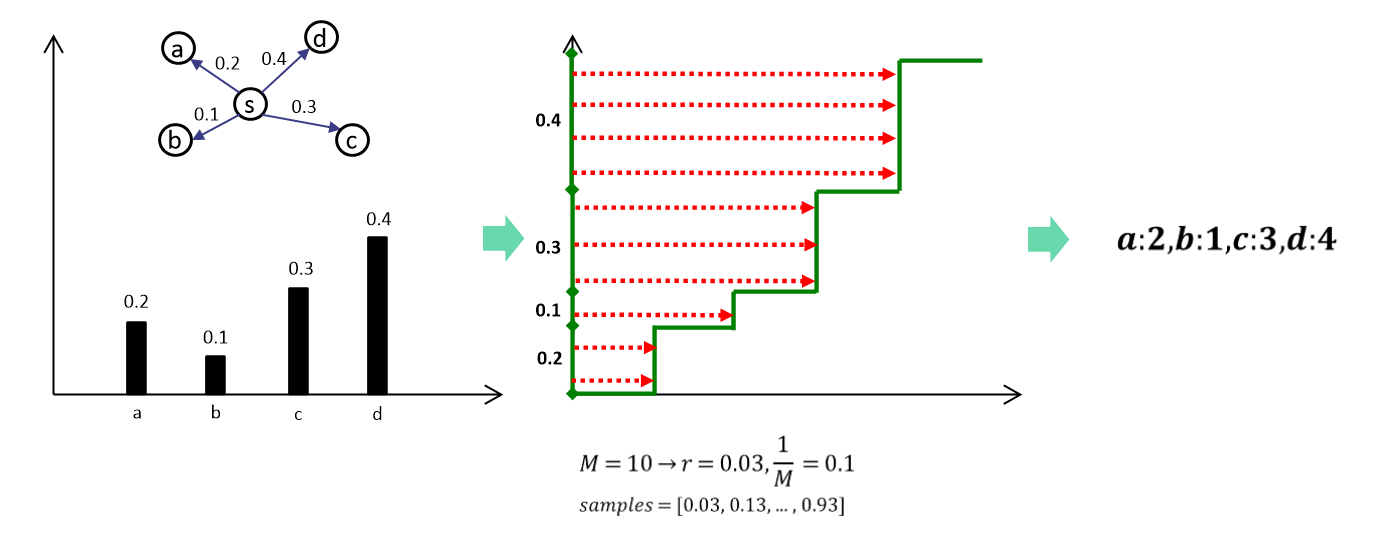
Experiments
NELL의 KB에서의 추론을 실험결과로 남긴다.
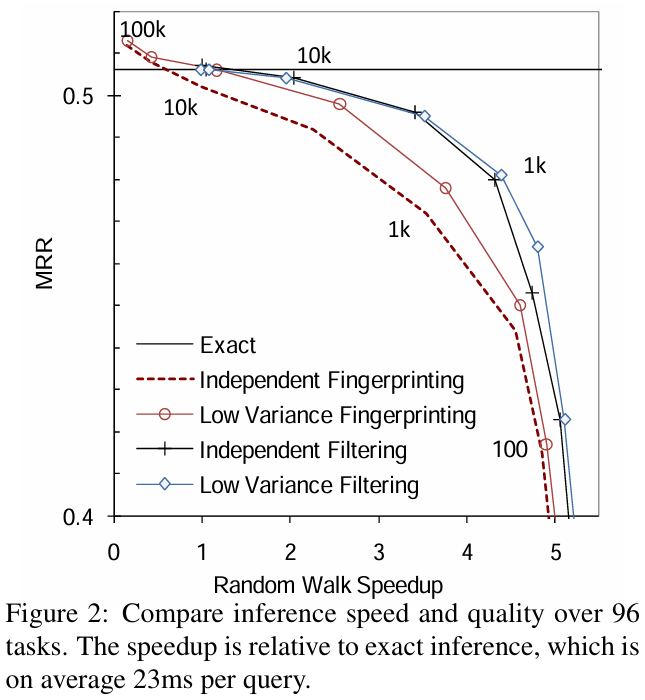
먼저 샘플링 전략에 따른 교차 검증 MRR이다. 여기서 x축인 speedup과 y축인 MRR 샘플링 속도와 정확도 사이의 trade-off관계를 잘 보여주고 있다.
위에서 진행한 교차 검증 결과는 KB가 완전하다는 가정하에서 진행한 것이다. 하지만 이는 사실이 아닌 경우가 많다. 따라서 Amazon Mechanical Turk service(MTurk)를 사용한 인간의 평가를 사용해 PRA과 N-FOIL의 추출한 rule의 성능을 비교한다.


$P_{majority}$는 쿼리 $R(a,?)$가 있을 때 가령 $R(a,?)$를 만족하는 쌍이 100개이고 이중 가장 많이 등장하는 쌍이 $R(a,b)$이고 그 쌍의 출현 횟수가 20이라면 $P_{majority}=0.2$가 되게 하는 것이다. 즉 이 값이 클수록 추론하기에 쉬운 쿼리이다. p@k는 precision at k라는 지표로 rank에서 상위 n개의 결과 중 유효한 결과의 개수를 n으로 나눈 값이다. 따라 클수록 좋다.

위는 RWR(Random Walk with Restart)과의 비교이다. 이를 통해 더 좋은 성능을 작은 시간적 희생을 통해 얻을 수 있음을 보여준다.
Conclusion
RNN기반의 rule mining 모델들과의 본질적인 차이점은 경로의 존재성에 더 집중한다는 것이지 결론적으로 추구하는 바는 동일하다. 기존의 PRA를 강화해 KB에서의 추론력을 향상한 의의가 있다.

