Paper :
Main interest
지식 그래프(Knowledge Graph, KG)는 일반 그래프의 특수 형태이다. 단순히 두 노드 사이의 관계를 무방향 간선 또는 방향 간선만으로 표현하는 것이 아닌 relation을 포함시켜 표현한다. 가령 두 entity $USA, Obama$사이의 관계를 지식 그래프에서는 $Obama\xrightarrow[]{hasNationality}USA$로 표현될 수 있는 것이다. 즉 일반 그래프보다 더 풍부하고 다양한 정보를 저장할 수 있는 것이 지식 그래프인 것이다.
지식 그래프에서 우리가 해결하고자 하는 문제는 크게 2가지이다. KG에 있는 두 entity사이에 있어야 할 relation이 무엇이냐를 추론하는 link prediction과 head entity와 relation이 주어졌을 때 tail entity에 올 노드를 추론하는 entity prediction 문제이다. 이 두 문제를 통틀어 knowledge graph completion 문제라고 부른다.

Problem with previous models
KG는 incomplete, noisy 문제가 만연한 데이터이다. 따라서 이를 해결하기 위해(KG completion이 필요한 이유이기도 함) 초기에 가장 인기 있었던 모델링 방법은 임베딩 기반 접근(Knowledge Graph Embedding, KGE)이었다. 즉 entity와 relation을 저차원 공간으로 매핑하는 방법을 취한 것이다. 하지만 이는 문제가 있다.
첫째, 설명 가능하지 않다. 이는 KGE에 한정한 문제가 아니다. 원래 임베딩이라는 것이 인간이 이해할 수 없는 결과물을 내놓을 수밖에 없기 때문이다.
둘째, transductive한 한계가 있다. KG는 거대한 만큼 매일매일 진화한다. 따라서 KGE의 경우 새로운 entity가 들어오면 모델이 작동하지를 않는다. 그에 해당하는 임베딩을 얻으려면 학습을 전부 다시 해야 한다.
이 문제에 국한되지 않는 모델을 만들고자 본 연구에서는 entity inductive한 모델을 만들게 된다. 하지만 아직은 relation한정 transductive 한 것이 아니냐고 생각할 수 있지만 KG에 entity는 새로 추가될지라도 새로운 relation이 추가되는 일은 드물기 때문에 모델을 inductive 하게 KG에 적용할 수 있다고 할 수 있는 것이다.
Architecture
본 연구에서는 두 entity 사이의 link prediciton에 집중한다(link preidction 문제는 entity prediction 문제로 둔갑 가능하다, 본 논문 2페이지 하단 참조). 본 연구에서 두 entity 사이의 link를 추론하기 위해 유의미하게 사용할 수 있는 정보는 두 가지가 있다고 주장한다.
1. Relational context
아래의 예시를 살펴보자 Ron Weasley와 Hedwig는 Harry Potter와 같은 relation으로 연결되어 있다. 그렇다면 $Pet\_Of$라는 relation은 누구와 연결되는 것이 더 자연스러울까? 이에 대한 정보는 그 entity에 연결된 relation들에 대한 정보들에 있다. Hedwig는 $Bought$로 연결되어 있기 때문에 "맥락상" Hedwig는 사물, 동물이고 Ron Weasley는 $Brother\_Of$로 연결되어 있기 때문에 "맥락상" 사람으로 인식할 수 있다.

즉 relational context는 entity의 type에 대한 정보를 함유하고 있다. 그리고 이 type에 대한 정보는 link의 종류에 대한 정보를 담고 있다고 볼 수 있다(Ron Weasley는 맥락상 사람이므로 $PetOf$는 맥락상 사물로 해석되는 Hedwig와 더 어울림).

위는 entity type에 대한 또 다른 예시이다. $h$는 그를 둘러싼 relation들을 기반으로 "사람"이라는 type를 유추할수 있고 $t$는 대학교임을 유추할 수 있다. 즉 이 정보들을 갖고 $h$와 $t$사이에는 $graduated\_From$ 등의 link가 존재할 가능성을 열어준다. 하지만 이런 노드의 type 정보만 갖고는 link 정보가 충분하지 않다. 어떤 사람은 그 대학을 졸업하지 않았을 수도 있고 어떤 사람은 대학을 아예 다니고 있지 않을 수도 있기 때문이다. 따라서 추가적인 정보, 즉 relational path가 필요하다.
2. Relational paths
Context는 entity의 응축된 정보를 갖고 있다. 따라서 context만으로는 $(h,t)$사이의 상대적 위치를 알 수 없다. 따라서 응축된 정보를 이어 줄 수단이 필요하다. 그것이 바로 relational path이다. $h$와 $t$를 잇는 경로들을 path라고 하며 이 특성들은 두 target 노드 사이의 관계를 표현한다.
총 정리하면 PathCon(PATHs and CONtext)아래와 같은 mechanism을 가진다고 볼 수 있다.

일단 통계적 수식으로 PathCon의 문제 해결 방식을 정당화해보겠다.
우리는 target entity가 주어졌을 때 relation을 알고 싶기 때문에 아래와 같이 쓸 수 있다.
$$p(r|h,t)\propto p(h,t|r)p(r)$$
$p(r)$은 relation의 prior distribution이므로 모델에 대한 regularization으로 작용할 뿐 우리가 크게 신경 쓸 부분은 아니다.
반면 $p(h,r|t)$는 다음과 같이 decompose 할 수 있다.
$$p(h,t|r)=1/2(p(h|r)p(t|h,r)+p(t|r)p(h|t,r))$$
위 수식이 모델 구축의 전반적인 방향을 제시하고 있다. $p(h|r),p(t|r)$은 relation이 주어졌을 때 entity에 대한 likelihood로 해석할 수 있다. 하지만 우리의 모델은 entity의 국한된 특정 정보에 집중하지 않기 때문에 entity를 local relational subgraph($C(\dot)$)로 대체해 표현한다. 이를 모델링하는 부분이 context 부분이라고 볼 수 있다.
$$p(h|r),p(t|r)\to p(C(h)|r),p(C(t)|r)$$
$p(h|t,r),p(t|h,r)$은 어떤 entity와 relation이 주어졌을 때 이와 관련 있는 entity에 대한 likelihood라고 볼 수 있다. 이는 path로 모델링할 수 있는 부분이다.
이제 relational context와 relational path가 어떻게 계산되는지 알아보자.
1. Relational context
전통적인 노드 message passing 방법과는 다르게 PathCon에서는 relation을 중심축으로 message passing을 진행한다. Naive 하게 아이디어만 가지고 온다면 아래와 같이 수식을 작성할 수 있다.

$N(e)$는 edge $e$와 최소 하나의 entity를 공유하고 있는 relation 집합이다. $s_{e'}^i$는 iteration $i$일때 edge의 hidden state이고 $m_e^i$는 edge $e$의 iteration $i$의 message이다. 모든 edge의 초기($i=0$) state는 원핫 벡터로 나타낸다. 전체적으로 아래와 같이 나타낼 수 있다.
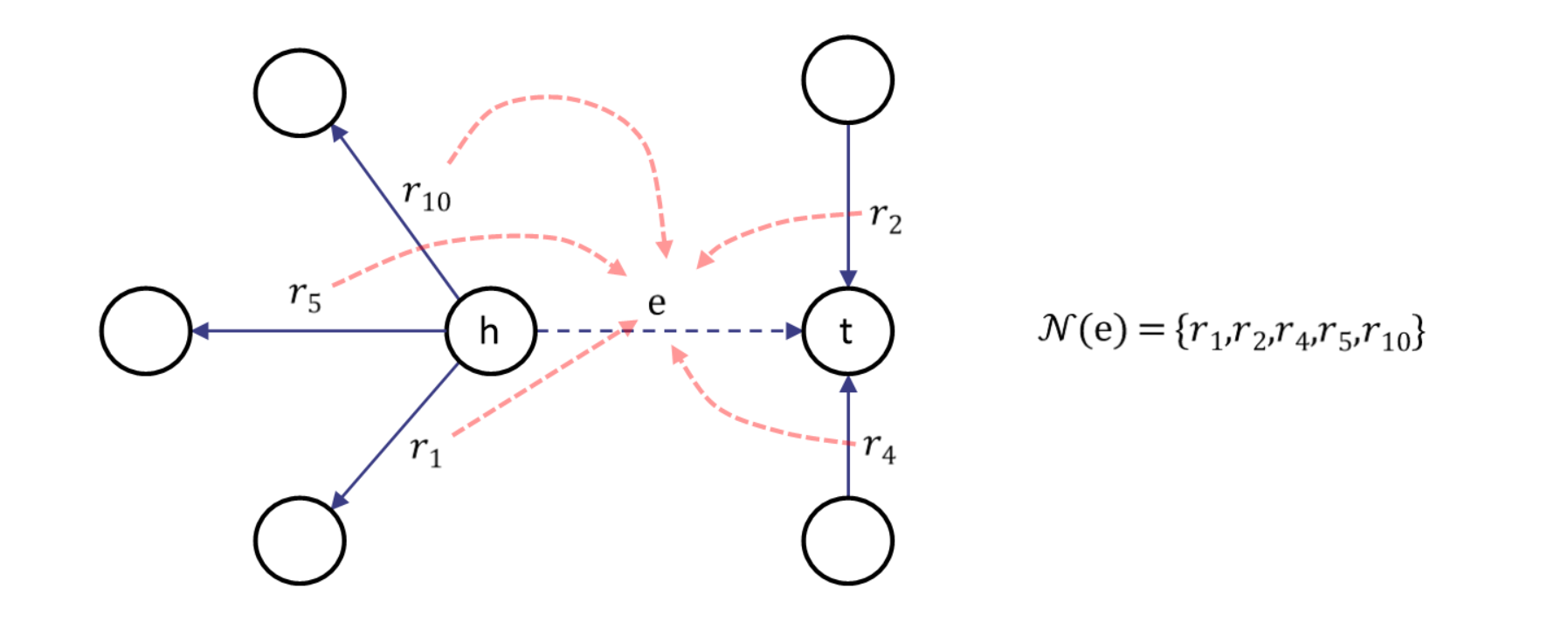
그러나 문제가 있다. 위처럼 node message passing 아이디어를 직접 갖고 온 relation message passing의 시간 복잡도는 nodes message passing($N$이 노드의 수, $M$이 edge의 수일 때 $2M+2N$)에 비해 더 크기 때문이다($Var[d]$가 노드 degree의 분산일 때 $NVar[d]+4M^2/N$, 이에 대한 증명은 본 논문 appendix에 있다). Relation message passing의 시가 복잡도를 잘하면 일차식으로 볼 수도 있지 않냐라고 할 수 있지만 KG의 노드 degree 분산은 매우 크다. 아래의 자료는 본 연구에서 사용한 데이터와 데이터의 내부 정보, train, validation, test 구성을 보여준다. 평균적으로 분산이 매우 큼을 알 수 있다. 사실 분산보다 더 중요한 것은 $M$ 값이 그래프에서 매우 크기 때문에 문제가 가정 컸던 것이다.

이 문제는 relational message passing 관점에서 relation(edge)가 노드가 되고 entity(노드)가 edge가 되기 때문에 생긴다. 즉 이런 그래프의 전환을 line graph라고 부른다. Line graph는 원본 그래프보다 더 복잡하기 때문에 다루기 힘든 점이 있다.
이 문제를 해결하기 위해 alternate relational message passing을 제안한다. 이는 시간 복잡도를 $6M$으로 획기적으로 줄였다. 그림으로 이해하는 것이 더 편하기 때문에 그림으로 설명하겠다.

먼저 노드마다 자신과 연결되어 있는 edge 정보를 노드가 각자 aggregate 한다. 이후 edge는 양 옆에 있는 노드 2개만 참조해서 aggregate 해주면 $e$의 message 계산이 완료된다. 큰 차이 없어 보이지만 노드를 "정보 분배의 중심"으로 해석한 이 방법의 시간 복잡도는 $6M$이다. 즉 node message passing의 시간 복잡도와 얼추 비슷함을 알 수 있다.
Aggregate는 입력 state들의 합으로 표현된다. 따라서 위 그림의 수식을 아래와 같이 표현할 수 있다.

$[\cdot]$는 concatenation을 뜻하고 $W^i,b^i$는 각 단계에서 weight matrix와 bias이고 $\sigma$는 비선형 활성화 함수이다.
위 과정은 $K$회 반복되고 마지막 message $m_h^{K-1},m_t^{K-1}$만이 $h,t$의 representation으로 선택된다.
2. Relational path
경로는 두 entity 사이의 상대적 관계를 나타내준다. 즉 $h$에서 $t$로 통하는 모든 경로의 집합을 $P_{h\to t}$라고 한다면 각 경로에 독립적인 임베딩 $s_P$를 부여할 수 있다(P\in P_{h\to t}). 하지만 서로 다른 경로의 개수는 관측하려는 경로의 길이에 따라서 기하급수적으로 증가한다. 가령 길이가 $k$인 모든 경로에 대한 임베딩의 개수는 $|R|^k$이다. 하지만 이는 실제 KG에서는 신경 쓸 필요가 없다고 연구자들은 주장한다. 이에 대한 근거로 FB15K에서 길이 2의 가능한 경로 조합 중 오직 3.2%만이 실제 경로로 존재한다는 것이 있다.
이제 context와 path를 합쳐 최종적으로 link prediction을 하는 방법에 대해 알아보자.
Target entity 2개의 최종 state를 갖고 $(h,t)$쌍의 state를 계산할 수 있다.
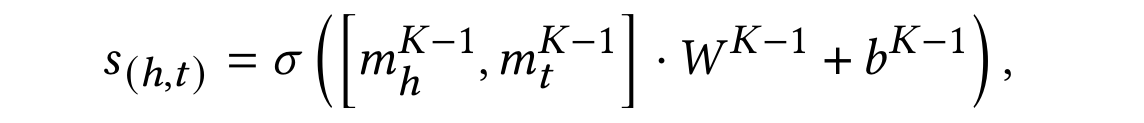
직전의 계산과 다른 점은 relation의 state가 들어가지 않는다는 것이다. 이는 relation이 train 과정에서는 보이면 안 되기 때문이다. 이렇게 계산된 $s_{(h,t)}$는 entity 쌍의 state라고 할 수 있다.
Path는 여러 개가 있을 수 있다. 모든 경로 벡터를 합해 path 집합의 최종 state($s_{h\to t}$) 낼 수도 있지만 $s_{(h,t)}$가 계산 되었으므로 entity 쌍의 state와의 유사도를 통해 path마다 attention을 계산할 수 있다.

$\alpha _P$는 경로 $P$의 attention score이다. 모든 경로의 상대적 attention을 구한 이후 아래의 계산으로 path 집합의 최종 state를 획득한다.
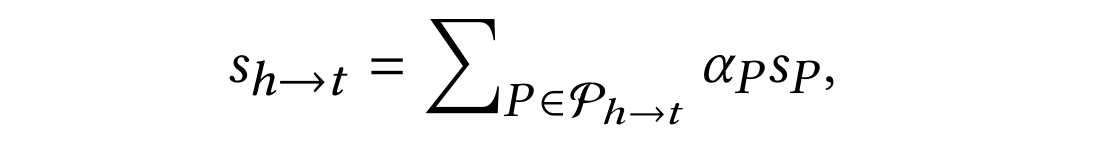
이제 마지막으로 context state와 path state를 합하여 softmax를 취하여 $p(r|h,t)$를 얻을 수 있고 loss를 최소화하는 방향으로 최적화를 해주면 된다.

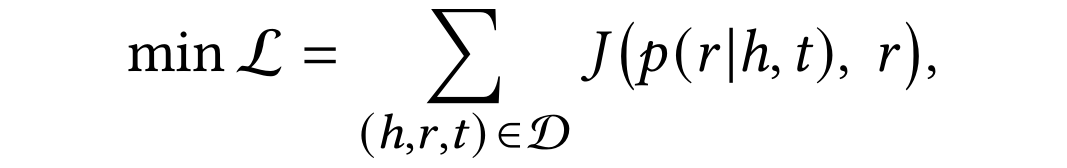
모델 설명은 여기서 사실상 끝난다. 하지만 모델의 구성중 일부 대안에 대해 비교 실험을 진행하기 때문에 그 대안들에 대해 살펴보겠다.
Mean context aggregator

Edge state 계산 시 concatenate 대신 평균을 취한다.
Cross context aggregator
추천 시스템의 combinatorial feature에서 영감을 받았다. Message에 있는 unit feature 사이의 상호작용을 반영한 matrix를 사용하는 방법이다.

마찬가지로 edge state 계산 시 사용된다.
Learning path represenation with RNN
경로마다 독립적인 임베딩을 부여해 주는 방법이 아닌 경로 $P(r_1,r_2,\dots)$에 있는 relation을 차례대로 RNN에 넣어 최종 path 임베딩을 얻는 방식이다. 파라미터가 고정되어 있기 때문에 공간적으로 매우 효율적이고 이미 여러 rule mining 기법들이 사용했던 방법이다.

Mean path aggregator
최종적으로 path 집합의 state를 계산할 때 attention을 계산하지 않고 그냥 다 더하는 방법이다. 이 방법은 context를 계산할 수 없을 때 사용할 수 있다는 점이 있다.
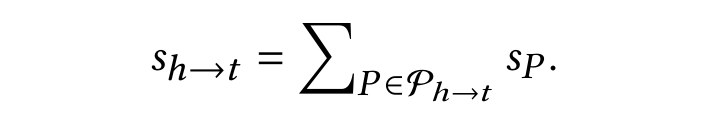
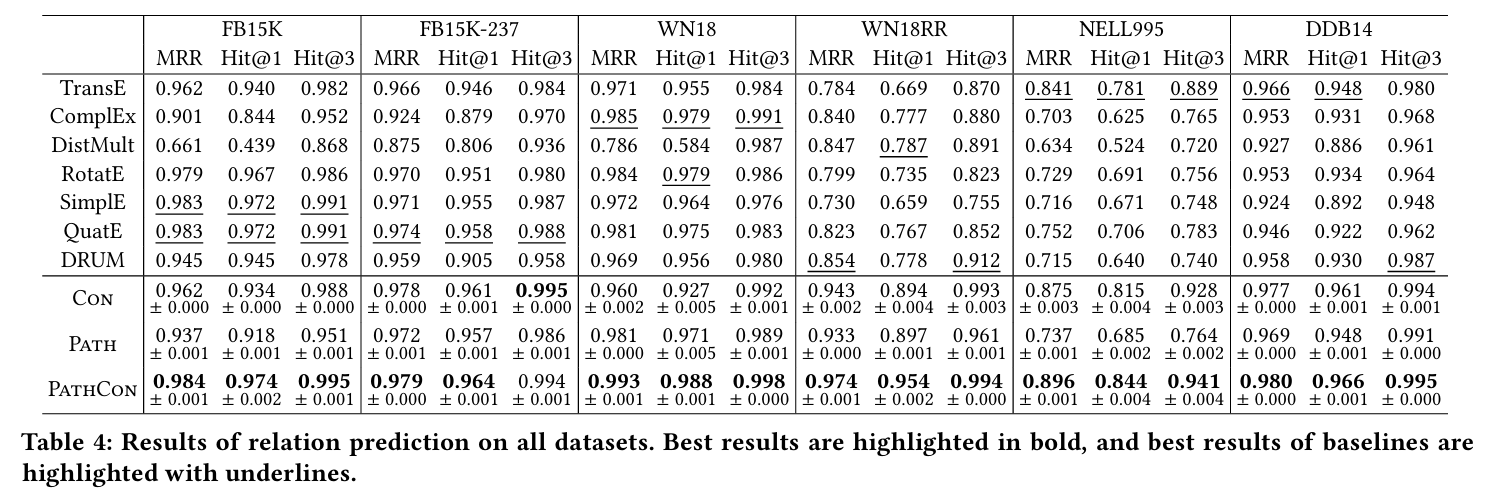
Experiments
Dataset은 FB15K, FB15K-237, WN18, WN18RR, NELL995와 본 연구의 연구자들이 제시한 데이터 DDB14를 사용하여 relation prediction과 inductive relation prediction을 실험한다. Metric은 MRR과 Hits@1,3이다. 3개 모두 높을수록 좋다. 또한 negative sampling을 훈련에 활용할 수 있는데 relation prediction을 수행하고 있기 때문에 정상적인 triplet을 $(h,r',t)$로 corrupt 시켜 negative sample을 얻는다.

위는 transductive setting에서의 실험이었고 이제 inductive setting에서의 결과를 보자. Inductive의 측정 방법은 test에 있는 노드 몇 개를 subset으로 sample 해 그에 해당하는 노드와 연결된 edge를 모두 train에서 지워버린다. 이때 지워지는 노드의 비율을 추적해 성능의 변화를 본다.

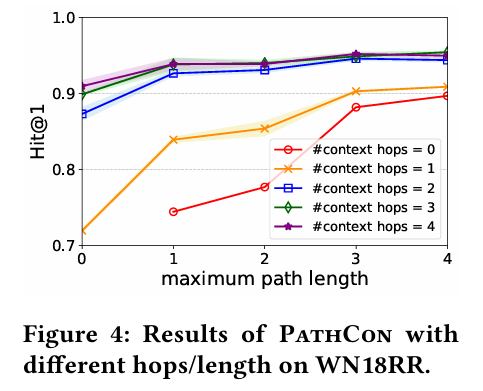
아래는 context message passing 과정에서 보는 최대 hop 수와 path 길이에 따른 Hit@1의 변화이다.
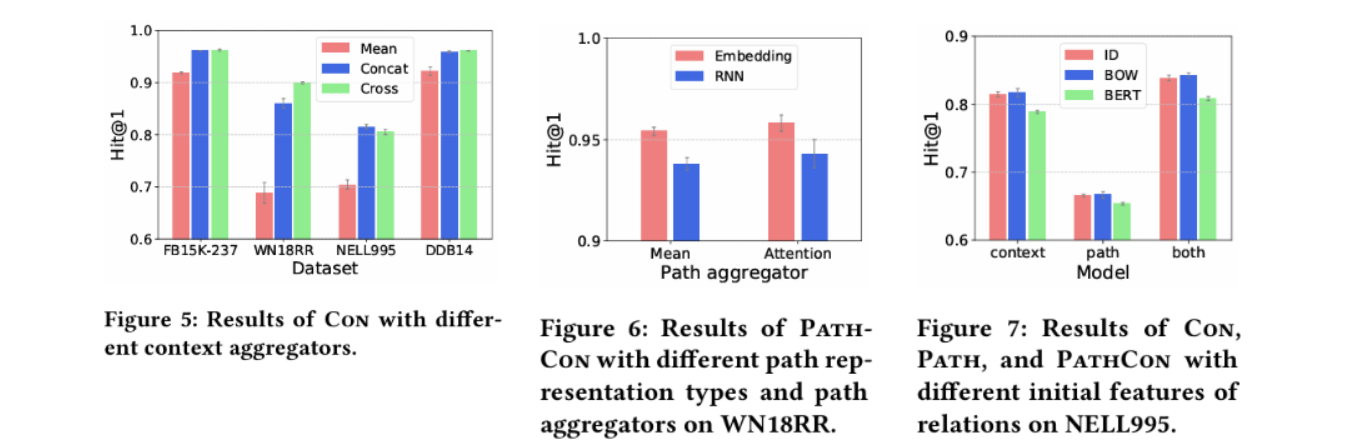
위는 design alternatives에 따른 결과이다. Context aggregator에서 Concat과 Cross가 서로 비등하지만 Cross는 차지하는 공간이 매우 많다. Path 임베딩의 경우 attention이 mean보다 언제나 좋은 성능을 보여주고 RNN은 independent embedding보다 나쁜 성능을 보여준다. 마지막으로 Figure 7은 edge 이름에 NLP 모델들을 적용하여 initial edge feature를 학습에 포함시키는 방법과 그에 따른 ablation study이다. ID는 원핫 임베딩을 지칭한다.
마지막으로 PathCon으로 학습된 특정 relation에 대한 중요한 context/path 정보들의 결과이다.

이를 마지막으로 PathCon은 설명 가능성을 겸비한 모델이라고 결론지을 수 있다.
Conclusion
Node message passing에서 아이디어를 가지고 와 KG에서 사용 가능한 alternate message passing 기법을 제시하였다. 이는 시간 복잡도를 획기적으로 줄일 수 있게 되어 강력한 contribution이라고 생각한다. 또한 relation prediction을 context, path 두 부분으로 나누어 기존의 path based 모델들처럼 path만 사용하지 않은 점이 모델의 강력함에 이바지한다. 기존의 KGE 접근들처럼 단순히 임베딩을 사용해 entity와 relation을 표현하는 것이 아닌 두 entity 사이에 존재할 relation에 대한 정보를 학습해 이후 KG에 새로운 entity가 들어와도 그 entity 주변에 link 정보들만 있다면 link prediction을 수행할 수 있는 inductive 성능도 확보하였다.

