4.4. Softmax Regression Implementation from Scratch — Dive into Deep Learning 1.0.3 documentation
d2l.ai
[1-1]
We can observe this code when we tamper with X
X_prob = softmax(X)
X_prob, X_prob.sum(1)
Instead of consisting X with small values such as torch.normal as the book did, let X be
X=torch.arange(90, 100).reshape(2, 5)
now, X consists of large values from 90 to 99, let's watch what happens to the resulting softmax.

This occurs because by summing up $e^{90}$ ~ $e^{99}$, overflow will likely occur.
[1-2]
We can experiment with this code.
X=torch.tensor([-103, -103, -103]).reshape((1, -1))
X_prob = softmax(X)
X_prob, X_prob.sum(1)
The funny thing I observed is that slight changes in values results in total domination by the biggest value. The result of the above code is

Now, let's change X to [-100, -103, -103] and see what happens.

As we can see, all the attention is directed to the first label. But this is not a surprise if we see the result with X being [4, 1, 1]. It is worth comparing these two since the difference between each values are the same.

Thus small negative values in classification is more preferable than large positive values. This can be proved by translation invariant. See 4.1.5, 6-4.
[1-3]
We only have to decrease all the elements by the biggest element. Thus we can achieve a new X that for each row(example), the biggest element is 0.
def softmax_fix(X):
for i in range(X.shape[0]):
X[i]=X[i]-max(X[i])
return softmax(X)
This new function can give more stable results than the previous function.
[2]
I don't fully understand the question since the loss function in the book already follows $\sum_iy_i\log\hat{y_i}$, where $y_i$ is the one-hot encoded answer tensor and $\hat{y_i}$ is the predicted softmax result.
[3]
It depands on what we are trying to classify. If it is for classifying clothes just like we did in the FashionMNIST, hard prediction(returning the most likely class) will be better than soft prediction(returning the softmax) because there is only one answer to the question. However in the perspective of medical diagnosis, soft prediction will be more desirable since the patient is unlikely to have only one desease.
[4]
Let's say we want to make a text finishing AI which recommends the next word the user would most likely use. By the context of softmax classification, we should get all the vocabulary in the dictionary and compute the possibility of each word. This is dawnting for the computer to accomplish since there are over million words in the dictionary and going through a certain algorithm to weigh them one by one is costly.
[5-1]
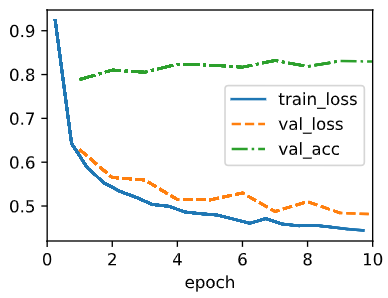

As for the learning rate, smaller learning rate results in a more smoother changes in validation, which is reasonable since it takes smaller steps than larger learning rates.
[5-2]
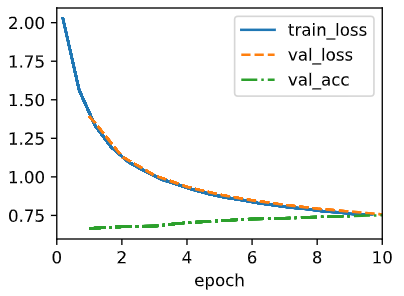
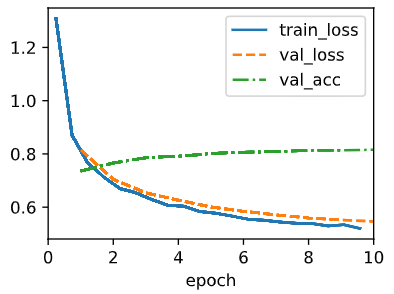

The efficiency between different batch_size are not that big since all of the val_acc's are distributed near 0.8. One thing to note is that when the batch_size is small the validation loss and accuracy seems to fluctuate a bit. This is because since the batch_size is small, there might be biased data in the minibatch.
'ML&DL > Dive into Deep Learning' 카테고리의 다른 글
| [4.3.4] Dive into Deep Learning : exercise answers (0) | 2024.03.03 |
|---|---|
| [4.2.5] Dive into Deep Learning : exercise answers (0) | 2024.02.29 |
| [4.1.5] Dive into Deep Learning : exercise answers (1) | 2024.02.25 |
| [3.7.6] Dive into Deep Learning : exercise answers (1) | 2024.02.15 |
| [3.6.5] Dive into Deep Learning : exercise answers (0) | 2024.02.15 |


