Paper:
Presentation content:
문제
지식 그래프(Knowledge Graph; KG)는 두 노드(entity) 간의 관계(relation)를 간선에 표현한 것이다. 아래의 예시를 보면 이해하기 편할 것이다.
그래서 우리가KG에서 해결하고자 하는 문제가 무엇인가? 물론 여러 가지 문제점이 있지만 본 논문에서 집중하고 있는 문제는 KG의 임베딩이다. 즉 entity와 relation을 임베딩한 상태에서 그들간의 관계를 학습하는 것이다.
기존에도 entity와 relation의 특성들과 연관성을 살리면서 임베딩을 하려는 노력들이 있었다. 하지만 기존 모델들에서 한 단계 더 나아가기 위해서는 다음과 같은 문제점들을 해결해야만 했다.
1. 얕은 추론 깊이
Neural network를 사용하기 이전의 모델들은 주로 entity와 relation의 관계를 벡터의 합성으로 포착하려고 했다. 이러한 벡터 관점에서의 해석을 이용한 기초적인 모델인 TransE를 살펴보자.
모든 entity와 relation을 같은 차원에 임베딩하고 가능한
$\vec{h}+\vec{r}\approx \vec{t}$을 만족하게끔 $\vec{r}$을 학습시킨다. 이러한 접근은 연산이 가볍다는 장점이 있지만 1-to-1 relation 이외의 relation은 학습하지 못한다(1-to-N, N-to-1, N-to-N).
2. Dataset 자체의 데이터 누수 문제
여태 읽은 논문 중에서 benchmark 데이터 자체에 문제를 제기한 논문은 처음본다. 그래서 evaluation에 사용하는 dataset자체에 어떠한 문제가 있는 것인가? 원인은 inverse relation에 있다.
만약 (A, owned-by, B)가 train set에 있고 (B, owns, A)가 test set에 있다고 가정하자. 학습 과정에서 (B, owns, A)는 절대로 보이면 안된다. 하지만 학습 과정에서 (A, owned-by, B)를 통해 자동으로 (B, owns, A)를 추론할 위험이 있다.
3. 파라미터의 개수 제약
다음 그림은 ConvE 이전의 효율적이다고 평가받는 모델 중 하나인 DistMult이다.
하지만 이도 문제가 있는게 결국 여기서도 $\vec{r}$이 파라미터인데 h, t와 차원이 동일해야 한다. 즉 파라미터 1개가 임베딩 차원 1개와 일대일대응 되어야 한다.
이는 KG를 학습함에 있어서 상당히 큰 제약으로 작용하는데, 그렇다고 무작정 임베딩 차원을 키울 수도 없는 꼴인데 왜냐하면 실제로 임베딩 차원이 200이면 benchmark dataset 중 가장 작은 규모인 FK15k에 대해서 33GB 크기의 임베딩 파라미터가 필요하기 때문이. 따라서 이를 극복하기 위해서는 임베딩 차원 크기와 파라미터 개수의 독립이 필요하다.
4. Multi-layer embedding의 overfitting 문제점
(Nickel et al. 2016)에서 소개하기로는 fully connected layer을 갖고 있는 multi-layer KG embedding모델은 overfitting에 취약하다는 사실을 밝혔다.
해결
1. 얕은 추론 깊이
단순한 벡터간의 합성 연산이 아닌 multi-layer propagation과 2D convolution을 통해 KG의 더 다양한 특성들을
학습할 수 있게 한다.
2. Dataset 자체의 데이터 누수 문제
Inverse relation을 제거한 새로운 dataset을 제시하고 향후 연구에서도 이를 사용하기를 권장한다. 실제로 inverse relation을 제거한 데이터에서의 학습은 모델의 정확도를 현저히 저하시킴을 evaluation 부분에서 볼 수 있다.
3. 파라미터의 개수 제약
Multi-layer를 사용하기 때문에 임베딩 차원 크기와 파라미터의 개수를 비교적 독립적이게 조절할 수 있다(아예 독립적이다라고는 말할 수 없는 게 NN의 구조상 어쩔 수 없다). 실제로 DistMult보다 17배 적은 파라미터로 동등한 성능을 내었다.
4. Multi-layer embedding의 overfitting 문제점
(Nickel et al. 2016)에서도 overfitting에 따른 여러 해결책들이 제시 되었지만 본 논문에서는 특히 dropout을 활용한다.
Architecture
바로 ConvE의 구조에 들어가기 앞서 왜 2D convolution을 하게 되는지 먼저 설명하겠다.
Convolution은 상당히 다양한 분야에서의 쓸모가 증명되었다. 이미지 인식부터 NLP까지 다양한 분야에서 좋은 성과를 보여줬다. 따라서 필자는 이를 KG에 적용해보자 한다.
우리가 다루고 있는 entity와 relation은 각각 단일 벡터이다. 행렬 관점에서 보면 1D라고 할 수 있다. 하지만 1D convolution의 단점이 있는데, 그것은 두 벡터의 관계의 접점 부분이 차원의 한계 때문에 제한적이라는 것이다.
이때 1D filter로 convolution을 하면 제한된 크기의 interaction 부분만 학습하게 되기 때문에 한계가 있다.
따라서 1D 벡터를 2D 벡터로 reshaping하는 임베딩 학습을 최초로 제안한 모델이 ConvE이다. 이를 통해 얻을 수 있는 장점은 더 넓은 interaction 부분을 학습할 수 있다는 점이다.
Interaction 부분과 필터의 시각화는 presentation ppt를 참고하기를 바란다.
이제 본격적으로 scoring function과 loss를 어떻게 계산하는지 살펴보자.
KG는 triplet을 하나의 원소를 갖으며 임베딩된 subject와 object entity의 임베딩 벡터는 $k$차원에 있다고 하자.
이제 우리가 계산할 score($\psi$)는 특정 triplet을 input으로 받으며 실수값을 점수로 output 한다.
눈여겨볼 점은 relation이 뭐냐에 따라 score 함수를 독립적이게 적용한다.
이것은 score function의 본체이다. 식만 봐서는 뭔 말인지 이해하기 힘드니 그림과 함께 살펴보자.
step1 : e1은 $\textbf{e}_s$이고 rel은 $\textbf{r}_r$이다. 즉 subject와 relation을 동일 차원으로 임베딩 해준다.
step2 : 2D로 reshape 하고 concatenate 한다. Experiment 데이터에 의하면 reshaping의 편리를 위해 처음부터 임베딩 차원 $k$를 $2^n$꼴로 맞춘다. 컨벌루션 직전에 drop out(20%만 drop out) 해준다.
step3 : 여러 개의 동일 크기 필터로 컨벌루션 해준다. 이를 통해 생성된 텐서를 다음과 같이 표현해 준다. Drop out(0.2)을 적용한다.
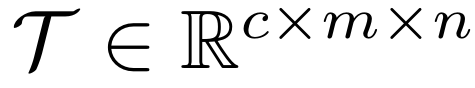
step4 : 텐서를 하나의 벡터로 변환시켜 준다($\mathbb {R}^{cmn}$). 이후 fully connected projection($\mathbf{W}\in \mathbb{R}^{cmn\times k}$)을 거친다. 따라서 결과적으로 $k$차원 벡터가 나오게 되는데, 크기를 기존의 임베딩들과 같게 해 준 이유는 이 새로운 벡터가 갖고 있는 의미는 "subject 임베딩과 relation 임베딩의 연관성을 반영한 벡터"라 할 수 있기 때문에 object 임베딩과 dot product를 수행하기 위해 동일 차원으로 만들어준 것이다.
내적의 연산적 허용과 맥락적 차원(e, r, o 간의 연결성)에 있어 $k$차원으로 최종적 임베딩을 하는 것은 충분히 납득 가능하다.
step5 : 살짝 그림과 수식이 맞지 않다. 분명 수식대로라면 실수값 하나만 나와야 하는데 그림에서는 여러 개의 결괏값(logit)이 보여진다. 그 이유는 논문에서는 1-N scoring 방식을 채택했기 때문이다. 이 방법은 1개의 s, r에 대해 여러개의 $\textbf{e}_o$를 한 번에 dot product 하여 여러 개의 score를 학습할 수 있는 방법이다. 이때 N은 training set에 있는 전체 entity다. 이에 반해 1-0.1N scoring(각 scoring 계산당 training의 10%만 사용)도 고려를 해보았지만 forward pass속도는 25% 빨라진 반면 수렴 시간은 230% 증가하여 이 연구에서는 1-N scoring을 고수한다.
step6 : score의 결과들을 logistic sigmoid에 통과시켜 주면 normalized 된 score가 나온다.
이제 loss function을 정의해 보자.
$t$는 정답 벡터다. s와 o가 r로 연결되어 있으면 1, 아니면 0.
Experiment
지표는 MR, MRR, Hits@k를 사용한다. MR은 작을수록, MRR, Hits@k는 클수록 좋다.
앞서 설명했듯이 DistMult보다 17배 적은 파라미터로 동등한 성능을 보인 것을 봐보자.
이제는 타 모델들과의 비교다.
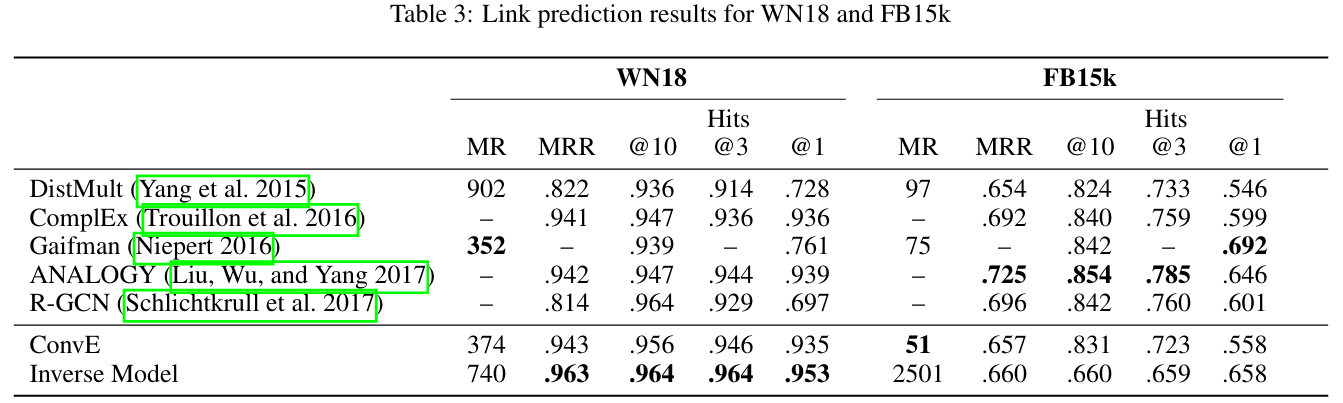
Inverse Model이 가장 좋은 성능을 보여주고 있다. 이때 Inverse Model은 순수히 inverse relation만 학습하게끔 이 연구에서 고안해 설계한 단순한 모델이다. 이를 통해 데이터 누수가 있는 것이 얼마나 큰 문제인지 알 수 있다.
WN18RR과 FB15k-237은 모두 WN18, FB15k에서 inverse relation을 전부 제거한 새로운 데이터이다. 이 경우 ConvE가 다른 모델들에 비해 고성능임을 알 수 있고 Inverse Model은 완전히 낮은 수준의 모델로 전락함을 알 수 있다.
Conclusion
ConvE는 기존 모델들의 한계를 극복하고 multi layer을 활용하여 KG의 다양한 특성을 학습하여 임베딩에 적용할 수 있다. 또한 2D convolution을 처음 사용한 모델로써 의의가 있다.
추가 분석
1D to 2D?
1D를 2D로 변형해도 되는 것인가? 생각해 보면 이상하다. 컨볼루션은 본래 특정 cell 주변의 cell들이 연관성이 있다는 전제가 있기 때문에 가능한 것이다. 따라서 NLP에서 주로 다루는 문장(1차원 배열)에서는 특정 단어에 대해 임베딩을 하기 위해 window size만큼의 이웃들을 aggregate해주는 전략을 취한다. 하지만 우리가 2D로 만들고자 하는 벡터는 feature 간의 그런 연관적인 특성이 전혀 드러나 있지 않다. 그래도 괜찮은 이론적인 이유가 뭘까?
내가 생각하기로는 1D 형태의 임베딩 벡터 자체가 갖는 의미보다 2D로 reshaping 된 벡터가 갖는 의미로 해석하는 편이 올바르다고 생각된다. 즉 우리는 1D로의 임베딩보다 2D로의 임베딩을 하고 있는 것이다.
왜냐하면 reshaping 과정에서 1D 자체가 가지는 정보가 모두 손실된다. 또한 컨볼루션을 수행하는 환경은 오직 2D에서만 이기 때문에 사실상 2D가 갖고 있는 정보가 ConvE에서는 전부다. 어차피 train과정에 있어서 filter size, embedding size, reshape size는 일정하기 때문에 일정한 학습이 이루어질 수 있는 것이다.
