Paper :
Presentation :
Main interest
지식 그래프란 두 노드(entity)가 특정 방향 간선(relation)으로 연결되어 있는 그래프 구조이다. 이때 데이터는 triplet(h, r, t) 꼴로 저장된다. 지식 그래프(Knowledge Graph ; KG)에서 수행하고자 하는 task들 중에서 가장 기반이 되는 것은 link prediction이다. 이는 entity와 relation 사이의 관계 패턴 학습하여 unseen link에 대한 추론을 하게끔 설계가 요구된다. 단순히 두 노드 간의 missing link를 추론할 수도 있지만 더 복잡한 관계(composition)의 추론도 이 task의 일부이다.
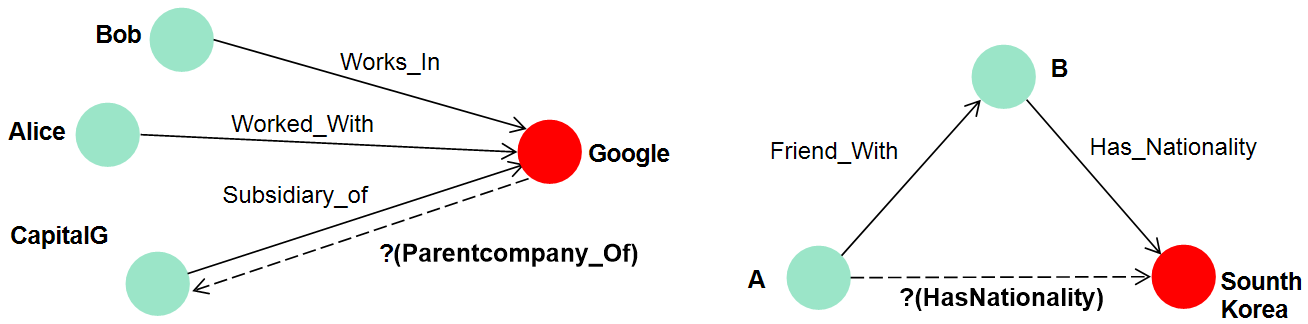
Problem with previous models
지식 데이터(Knowledge Base ; KB)들은 크기가 거대하기 때문에 모델의 시공간 복잡도는 KB의 크기에 linear해야 한다. 초기 모델들(RESCAL, SE)은 tensor factorization과 같은 무거운 접근 방법들을 사용하였지만 점차 모델들이 가볍게(TransE, DistMult) 변화하였다. 하지만 모델이 가벼워진 만큼 데이터의 다양한 특성들을 기대만큼 흡수하지 못한 문제점들이 있었다. 따라서 연구자들의 목적은 가벼우면서도 그래프의 다양한 표현들을 학습할 수 있는 방향으로 굳어졌다.
따라서 relation을 어떤 방식으로 임베딩할 것이냐가 주 관심사이다. 왜냐하면 entity사이에 의미를 심어주는 징검다리 역할을 하는 것이 relation이기 때문에 임베딩 된 entity와 relation 사이의 관계를 학습하는 것을 목적으로 취한다. Link predictoin에서 추론하고자 하는 Relation의 종류는 여러 가지가 있겠지만 크게 4 가지(symmetry/antisymmetry, inversion, composition)에 대한 학습을 목표로 한다. 고작 4개를 기준으로 모델링하는 이유는 이들은 전체 관계들에 대해 포괄적인 개념들이기 때문이다.
RotatE가 나오기 전까지 위의 4가지를 모두 학습할 수 있는 모델은 존재하지 않았다. 임베딩 벡터들의 합성으로 관계들을 학습한 TransE는 모델의 가벼움으로 각광받았지만 symmetry를 학습하지 못한다. 이후에 나온 DistMult는 TransE를 보완하고자 관계들의 대칭을 전제하고 삼중 점곱으로 모델을 구성하였지만 이는 결국 symmetry밖에 학습하지 못하는 장애물이 되었다. 이후에 ComplEx는 임베딩을 복소 공간으로 확장하여 symmetry, antisymmetry, inversion까지 학습이 가능하게 하였지만 여전히 composition을 학습하지 못했다.

자세히 무엇 때문에 한계가 있는지 확인해보자.
TransE의 경우 symmetry를 제외한 나머지 3개의 relation에 대한 학습이 가능하다. Symmetry 학습에 실패한 이유는 $\textbf{h}+\textbf{r}\approx \textbf{t},\textbf{t}+\textbf{r}\approx \textbf{h}$를 동시에 만족시키기 위해서는 $\textbf{r}=\textbf{0}$을 만족해야 해서 결국 $\textbf{h}=\textbf{t}$가 되어버리기 때문에 symmetry관계를 학습할 수 없다. Symmetry 관계가 데이터에 '존재한다고만 해서' 두 entity 임베딩을 같게끔 만들라는 이유는 전혀 없다.
DistMult는 이러한 TransE의 한계를 극복하고자 약간 극단적인 방법을 취했는데, symmetry relation 이외는 전혀 학습 못하는 모델을 만들었다. 두 entity와 relation에 대해 삼중 점곱(score function(이 증가하는 방향으로 학습) : $f_r(h,t)=<\textbf{h},\textbf{r},\textbf{t}>=\sum _i h_ir_it_i$)을 수행하여 연산의 순서가 없기 때문에 antisymmetric($<\textbf{h},\textbf{r},\textbf{t}>=<\textbf{t},\textbf{r},\textbf{h}>$), inversion($<\textbf{h},\textbf{r}_1,\textbf{t}>=<\textbf{t},\textbf{r}_2,\textbf{h}>\therefore \textbf{r}_1=\textbf{r}_2$)을 학습하지 못한다. Composition의 경우 DistMult 논문에서 가능하다고 설명하였지만 현실적으로 충족하기 힘든 가정에 기반하기 때문에 불가능하다고 평가받는다.
이를 보완하고자 DistMult에서 영감을 받아 복소 공간으로 확장한 ComplEx는 composition을 제외한 모든 relation을 학습할 수 있게 되었다. Complex 수식 특성상($f_r(s,o)=Re(\textbf{e}_s\textbf{W}_r\bar{\textbf{e}}_o)$) 두 수식을 접합할 수 없기 때문이다.
Architecture
RotatE는 임베딩을 복소평면에서의 회전으로 표현한다. 즉 entity와 relation 임베딩들이 요리조리 회전하면서 다음 수식을 만족하게끔 학습되는 것이다.
$$\textbf{h}\circ \textbf{r}\approx \textbf{t}$$
위의 수식에서 $\circ$는 Hadamard(element wise) product이고 $h_i,r_i,t_i\in \mathbb{C},|r_i|=1$일 때$t_i=h_ir_i$ 등식을 만족하기를 바란다.
따라서 RotatE의 score function은 다음처럼 쓸 수 있다.
$$f_r(h,t)=-\left\| \textbf{h}\circ \textbf{r}-\textbf{t}\right\|$$
이 접근이 효과적인 이유는 임베딩 차원이 1인 극단적인 경우를 TransE와 비교해서 살펴보자.

TransE의 경우 1차원으로 임베딩 되어 한낱 직선 위를 움직이는 벡터들로 임베딩 되었지만 RotatE의 경우 복소 공간에 놓여있기 때문에 다양한 벡터들을 표현할 수 있게 되어 다양한 특성들을 표현할 수 있다.
또한 특수한 가정 없이도 symmetry/antismmetry, inversion, composition을 학습할 수 있음을 증명할 수 있다. 참고로 Hadamard product는 결합 법칙이 성립하기 때문에 아래의 증명들은 비교적 간단하게 풀린다. '^'는 논리 AND 기호이니 오해 없길 바란다.
1. Symmetry
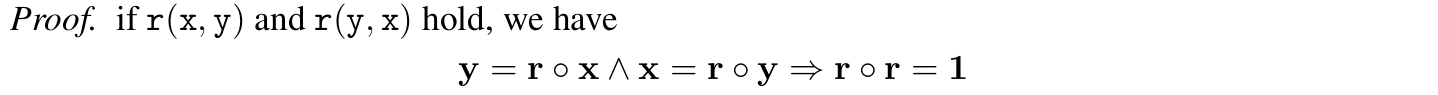
$r_i=e^{i\theta_r}$
$r_i\circ r_i=e^{2i\theta_r}=1\Rightarrow \theta_r=0,\pi$
2. Antisymmetry

$\theta_r\neq 0,\pi$
3. Inversion

$r_{1i}r_{2i}=e^{i(\theta_{1r}+\theta_{2r})}=1\Rightarrow \theta_{1r}+\theta_{2r}=0,2\pi $
간단히 말해 $r_{1i}=\bar{r_{2i}}$.
4. Composition

$\theta_{1i}=\theta_{2i}+\theta_{3i}$
RotatE는 TorusE의 일반적인 경우이다. TorusE는 임베딩 벡터들을 torus(입체 도넛) 위에 위치시키기 때문에 compact Lie group에서 임베딩을 해석했다고 할 수 있다. 이 모델의 경우 임베딩 벡터의 크기를 고정시키지만 RotatE는 relation 벡터만 1로 고정시킨다.
손실 함수는 다음과 같은데

거리 함수($d_r$, $L1$-norm을 사용)와 positive sample, negative sample에 대해 정의되어 있다. 자세히 보면 negative sample의 손실 평균을 내고 있지 않은 것을 보아 $k$는 하이퍼 파라미터임을 유추할 수 있다.
하지만 uniform 하게 뽑은 negative sampling은 문제가 있다고 주장한다(사실 이 문제 제기는 KBGAN에서 최초로 하였지만 RotatE에서 negative sampling을 하는 GAN모델의 학습법을 살짝 바꾸었다). 문제가 뭐냐면, negative 한 sample 중에서 터무니없이 틀린 triple이 들어 있는 경우 negative part의 $log$ 값이 커져 결국 loss의 감소에 기여할 것이고 이에 따라 positive sample은 필요만큼 penalize 되지 않을 것이다.
그래서 나온 접근이 self-adversarial(자기 적대적) negative sampling이다. 이는 그 순간에서의 임베딩 모델의 학습 현황에 따라 negative sample들에 가중치를 부과해 주는 것이다.

즉 샘플링된 negative sample에 대해서 "명백히 틀린" 데이터에 낮은(여기서는 distance가 아니라 score을 사용한다) 가중치를 부과하여 영향력이 작게끔 조절한다. 반면에 생성된 sample에 대해 높은 score을 보이는 negative sample이 있다면(여기서 '이 triple은 실제로 참일 수도 있지 않나?'라고 생각하면 안 된다. Negative sample은 전부 틀린 데이터(closed-world assumption)라고 가정하기 때문이다) 모델이 크게 혼나야(?) 하기 때문에 큰 가중치를 부과해 큰 loss로 이어질 수 있게 한다.
따라서 최종 형식은 다음으로 바뀐다.
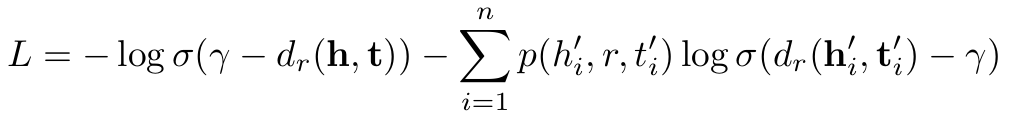
계산이 uniform 방식보다 더 요구되지만 이후 experiment에서 성능 향상을 보여주었다.
Experiments
사용할 dataset의 특징들에 대해 살펴보자.
FB15k, WN18 - symmetry, antisymmetry, inverse pattern을 학습하기에 좋음
FB15k-237, WN18RR - 위의 데이터에서 inverse relation만 제거하여 symmetry, antisymmetry, composition 학습에 좋음
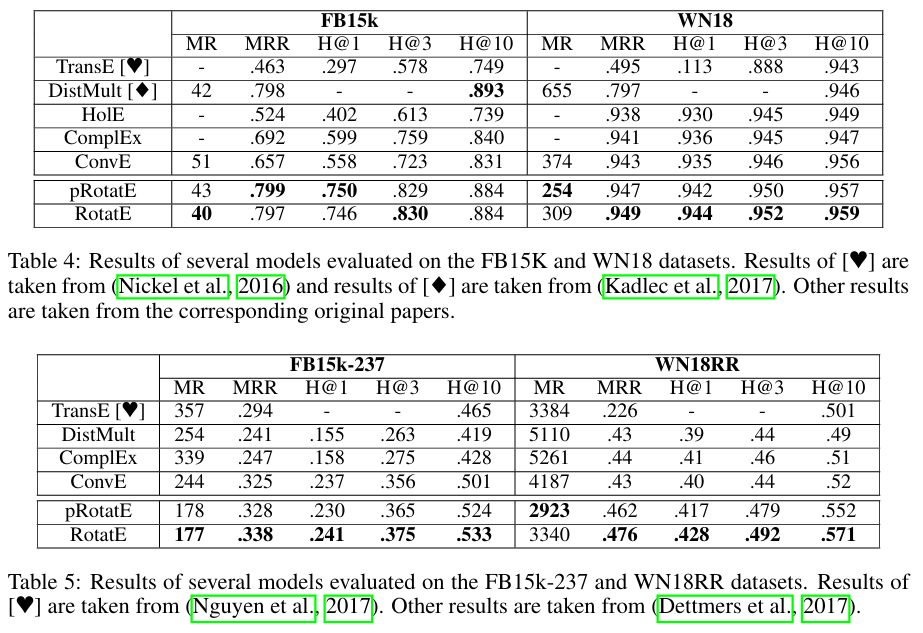
여기서 pRotatE는 RotatE와 같은 모델 구조를 가지지만 entity 벡터의 크기를 특정 상수로 고정시킨 모델이다(relation 임베딩 크기는 여전히 1로 하면서). 하지만 논문의 appendix에서 증명하기를 이 고정 상수값이 커질수록 모델이 TransE로 퇴화될 수 있음을 보였다. 직관적으로 봤을 때 TransE로 퇴화하는 이유는 벡터의 크기가 커질수록 벡터의 회전은 선형적인 행보를 보일 가능성이 있다. 우리의 지구도 얼핏봤을 때는 평평해보이지만 이는 지구가 워낙 거대해서 생기는 착시인 것처럼 RotatE도 그런 착시가 발생할 수 있다는 것이다.
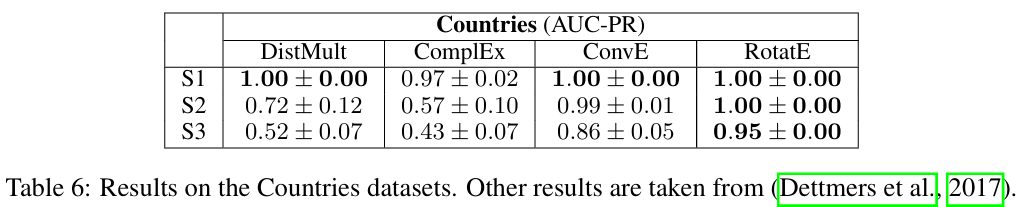
Table 6는 composition에 특화된 Countries에 실험을 수행한 결과이다. S#는 길이가 #인 composition을 포착할 수 있는지에 대한 정확도이다. RotatE가 나머지 모델들을 압도함을 알 수 있다.

보면 symmetry인 similar_to는 앞서 증명한 symmetry의 조건을 충족하고 있음을 알 수 있고 hypernym의 inverse relation인 hyponym의 관계도 명확히 (c)를 통해 알 수 있고 (g)에서 composition을 증명해주고 있다.

위는 negative sampling technique에 따라 학습을 달리 한 것이다. 결과를 보면 성능이 향상됨을 알 수 있다.
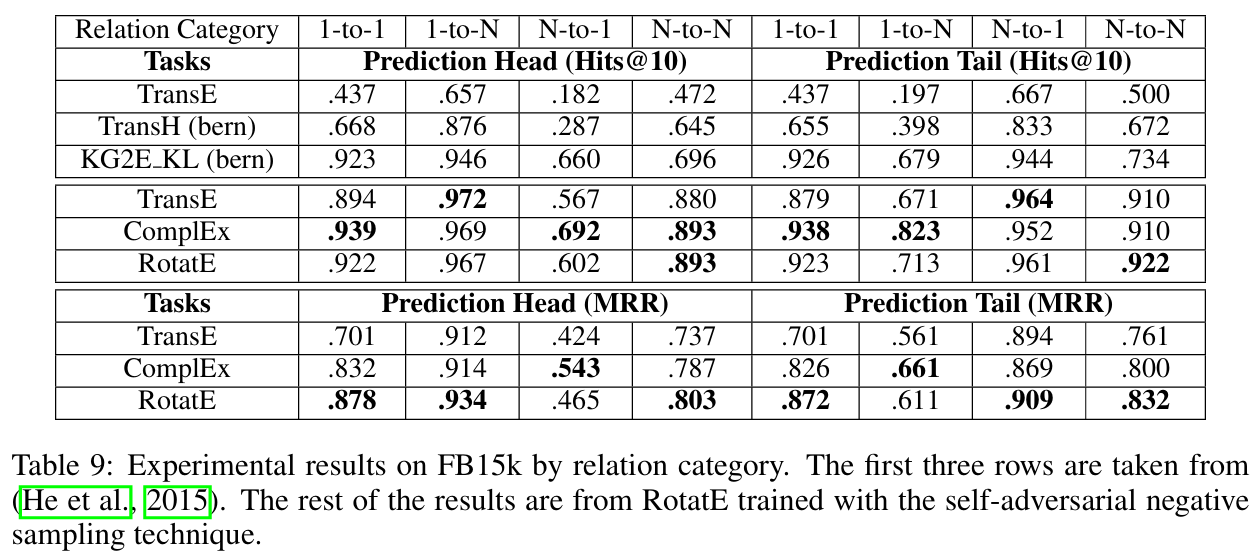
이는 self-adversarial negative sampling을 적용한 N-to-M 학습의 결과이다.
Conclusion
Symmetry, antisymmetry, inversion, composition을 모두 학습할 수 있는 모델을 최초로 고안했음에 의의가 있다. 또한 모델의 크기가 KB의 크기에 선형적으로 증가하므로 더 거대한 KB에 대해서도 general 하게 사용할 수 있음을 알 수 있다.



