Paper :
Presentation content :
Main interest
지식 그래프(Knowledge Graph ; KG)는 subject entity에서 object entity로 linking 하는 relation으로 이루어져 있는 방향 그래프이다. 예를 들어 "A는 B나라에서 태어났다"라는 사실을 KG에서는 (A, IsBornIn, B)와 같이 triple 꼴로 데이터를 저장한다. A, B는 노드이고 "IsBornIn"은 간선의 종류가 된다. 이와 같은 방식은 사실 기반 데이터들을 효율적으로 저장하는 방법이기 때문에 추천 시스템, 추론, NLP와 결합하여 사용되기 때문에 다양한 분야에서 활용될 수 있다.
하지만 KG는 거대하고 미완성이며 시간이 지남에 따라 규모가 커진다. 이러한 문제점을 knowledge graph completion이라고 하고 KG에서 해결하고자 하는 여러 문제점들 중 가장 기초적인 문제이다. 본 논문에서는 이 문제를 특히 link prediction에 초점을 맞혀 해결하고자 한다. Link prediction은 entity 간의 비어 있는 relation을 채워주는 작업을 말하는데, 앞에서 언급한 미완성 문제를 해결하기 위한 것이다. 또한 knowledge base(지식 그래프 데이터 ; KB)는 규모가 매우 크기 때문에 다양한 크기의 그래프에 대해 general 하게 적용할 수 있는 가볍고 효율적인 모델을 만드는 것이 우리의 목표이다.
Problems with previous models
Completion을 위해 우리는 entity(노드)와 relation(간선)을 벡터 또는 행렬로 저차원 임베딩하고 학습을 시킨다. 이 저차원으로 projection 하는 방법은 KG에서 뿐만 아니라 NLP, Graph 분야에서도 매우 성공적인 업적을 올렸기 때문에 우리는 어떻게 entity와 relaiton을 잘 표현할 수 있는 방법을 학습하는 것을 목적으로 한다.
이전의 모델들을 살펴보기 앞서 scoring function에 대해 알고가자. Scoring function은 두 entity 임베딩과 relation 임베딩이 얼마나 높은 연관성을 보이는지 실수값을 반환하여 함수이다. 여기에다가 logistic function을 씌우면 점수를 확률로 변환하고 정답 값(link가 실제로 존재하면 1, 아니면 0)과 비교하여 학습할 수 있게 된다.
이 연구에서 기존의 강력했던 모델들과 각 모델의 scoring function, relation parameter과 시공간 복잡도를 표로 제공해 주었다.
그래서 기존 모델들의 문제가 무엇인가?
Dot product로 구성한 scoring function(NTN, DistMult, HolE)은 매우 성공적이었다. 왜냐하면 자연히 행렬곱과는 다르게 가벼웠고 symmetry와 (ir-)reflexivity relation을 포착할 수 있었기 때문이다. 하지만 antisymmetric relation을 학습하기에는 모델의 능력 범위 외였다. 이를 포착하려면 모델을 더 복잡하게 만들어야 하는데 overfitting 위험을 감수해야 했다. 이러한 이유 때문에 parameter 규모와 모델 성능 사이의 저울질이 매우 중요하다.
여기서 ComplEx는 근원적인 수학적 철칙에서 해결의 실마리를 발견한다. 결론적으로 ComplEx는 복소 공간으로의 확장으로 dot product의 가벼움을 수용했을 뿐만 아니라 antisymmetric relation까지 학습할 수 있는 모델을 만들어 낸다.
How "ComplEx" can fix it
이 섹션에서는 ComplEx의 구체적인 내부 구조에 앞서 왜 ComplEx가 자연스럽게 발상되었는지 수학적으로 설명할 것이다. 최종 architecture은 다음 섹션에서 다루겠다.
특정 1개의 relation $r$에 대해 $\left| \varepsilon \right|=n$의 entity 집합($\varepsilon$)이 있다고 하자. Subject $s\in\varepsilon$와 object $o\in\varepsilon$의 연결 여부를 이진 값($\textbf{Y}_{so}\in \left\{1, -1\right\}$, $\textbf{Y}\in \mathbb{R}^{n\times n}$)으로 나타낼 수 있다. 즉 인접행렬로 이해할 수 있다, 연결이 있으면 1, 없으면 -1
이에 대해 우리가 두 entity와 $r$의 연관성을 측정한 latent score matrix($\textbf{X}$)가 있다고 하자.
$$P(\textbf{Y}_{so}=1)=\sigma (\textbf{X}_{so})\cdots (1)$$
즉 연결성이 있는 두 entity에 한해서 normalize 되기(logistic에 의해) 직전의 score를 갖고 있는 행렬을 $\textbf{X}\in \mathbb{R}^{n\times n}$ 라고 할 수 있는 것이다.
결론적으로 $\textbf{X}$는 $\textbf{Y}$에 의존하며 실전 training 과정에 빗대어 표현하면 $Y$는 부분적(모든 데이터가 training에 있지는 않으므로)으로 관측된 sign matrix(부호 행렬, 부호로 이루어진 행렬이라 할 수 있다. 우리의 경우 relation과의 연결 유무에 따라 1, -1로 표현할 수 있고 더 나아가 0으로 '비어 있다'를 표시할 수 있다. 여기서는 일단 1, -1에만 집중한다)라고 할 수 있다.
우리의 진짜 목적은 실세계 KB에 대한 근사가 유연한 일반적인 $\textbf{X}$의 구조를 찾고 싶은 것이다. 왜냐하면 아까도 언급했듯이, $\textbf{X}$는 scoring function이고 이는 우리가 구하고자 하는 것이기 때문이다. 더 간결히 표현하자면 기존의 접근들은 연산들을 통해 scoring function을 만들고 $\textbf{X}$를 구축했지만 여기서는 $\textbf{X}$를 수학적으로 분해해 justified 된 scoring function을 역으로 구축한다. 마치 기존의 접근은 bottom-up이었다면 ComplEx에서는 top-down 방식을 취한다. 결과적으로 이 접근법은 견고한 모델을 만들어냈고 우연치 않게 DistMult의 antisymmetric 문제가 있는 이유까지 증명한다.
그래서 이제 우리는 $\textbf{X}$를 어떤 방식으로 분해할까 고민한다. 가능하면 factorize(곱의 꼴로 분해, 본래 의미는 '인수분해') 하고 싶다. 앞서 dot product의 장점을 설명한 것이 이유이다.
일단 첫 번째 시도는 두 행렬 곱으로의 분해이다.
$$\textbf{X}=\textbf{U}\textbf{V}^T\cdots(2)$$
$\textbf{U},\textbf{V}\in \mathbb{R}^{n\times K}$, 두 행렬은 기능적으로 독립이며 $K$는 $\textbf{X}$의 rank이다. 기능적으로 독립(functionally independent)이란 서로의 변화나 update에 영향을 주지 않는다는 것이다. 이를 통해 $\textbf{U}$를 subject, $\textbf{V}$를 object entity로 생각해 보면 어떤 특정 entity의 임베딩이 subject에 오냐 object에 오냐에 따라 다르다는 것을 추정할 수 있다.
하지만 link prediction에서 같은 entity가 subject에 올 수도 있고 object에 올수도 있다((A, LiveIn, B), (B, CityOf, C)). 위치에 따른 임베딩이 다르면 임베딩을 만듬에 있어 일정하지 않고 데이터의 양도 많이 필요하기 때문에 저저는 통일된 임베딩을 만들자고 제안한다.
따라서 두 번째 시도는 고윳값 분해로 넘어간다.
$$\textbf{X}=\textbf{E}\textbf{W}\textbf{E}^{-1}\cdots(3)$$
Dot product를 유지하면서 subject, object 임베딩이 서로 dependent 한 방식이기 때문에 맥락상 첫 번째 시도보다 적절한 factorization라고 할 수 있다. 고유 분해는 정방 행렬($\textbf{X}$)에 대한 실공간(real space)에서 가능하고 분해된 3개의 요소들 또한 같은 공간 안에 있다. 하지만 고윳값 분해에서 역행렬을 매번 구하기 매우 힘들기 때문에(거의 $O(n^3)$) $\textbf{X}$를 대칭 행렬이라고 가정한다.
이 가정을 하면 아주 편리해지는데, $\textbf{X}$가 orthogonal 해져 $\textbf{E}^{-1}=\textbf{E}^T$가 성립하기 때문에 연산량을 대폭 줄일 수 있다. 하지만 우리의 이후 score matrix가 될 행렬이 반드시 대칭이어야 하는 제약 조건이 있기 때문에 이 접근은 antisymmetric 한 relation을 학습할 수 없다.
대칭, 비대칭 관계를 모두 포착하기 위해서는 실공간에서 복소 공간으로의 이동을 제안한다. 즉 임베딩이 $x\in \mathbb{R}^k$로 나타낼 수 있는 공간에서 생각해 보자는 것이다.
하지만 먼저 복소 공간에서는 우리가 애용하던 dot product가 안 먹힌다. 왜냐하면 실공간에서는 $x^Tx=0$은 벡터가 영벡터임을($\left\| x\right\|=0$) 함축했지만 복소 공간에서는 벡터의 크기가 0 임을 보장하지 못한다. 즉 normalization 등에 사용을 못한다. 그래서 우리는 에르미트 내적(Hermitian product)을 사용할 것이다.
$$<u,v>:=\bar{u}^Tv\cdots(4)$$
$u$와 $v$는 복소 벡터이고 벡터 $u$로 설명하자면 $u=Re(u)+iIm(u)$로 나타낼 수 있고 $Re(u),Im(u)\in \mathbb{R}^K$이다. 즉 에르미트 내적을 사용하면 $\bar{x}^Tx=0$가 영벡터임을 잘 나타내어 위상적인 norm을 잘 나타낼 수 있음을 알 수 있다.
자, 그래서 복소 공간으로 이동한 이유는 무엇인가? 역행렬을 구하기 싫고 대각 행렬로 제약을 걸기어서 모델의 성능도 제한시키고 싶지 않았던 것이다. 그래서 논문에서 내린 가정은 "$X$는 복소 공간에서의 normal matrix이다"를 가정하면서 모든 것이 해결된다.
$$X=\textbf{E}\textbf{W}\bar{\textbf{E}}^T\cdots(5)$$
왜냐하면 $X$가 normal matrix임과 $X$가 유니터리 대각화 가능하다와 동치이기 때문이다.
유니터리 대각화의 장점은 다음과 같다.
1. 유닛화 가능. $E$는 orthogonal 하기 때문에 역행렬을 켤레 전치 행렬로 대체할 수 있다.
2. 대각화 가능. 고윳값 분해처럼 분해할 수 있다.
하지만 score은 실수여야 하므로 실수 부분만 갖고 온다.
$$X=Re\left(\textbf{E}\textbf{W}\bar{\textbf{E}}^T\right )\cdots(6)$$
결국 우리는 이론적으로 normal하지 않은 어떤 실공간의 행렬 $X$에 대해서도 분해를 할 수 있음을 정당화하였다.
결론적으로 우리는 (2)에서 (6)까지 유도함으로써 얻은 장점은
1. $X$를 대칭 행렬로 한정하지 않아도 antisymmetric relaiton까지 학습할 수 있다.
2. 계산적으로 단순함을 유지하였다.
3. 어떤 실공간 행렬에서도 사용할 수 있으므로 일반화된 모델을 얻었다.
4. $E$의 행 벡터는 $X$의 각 행, 열에 대응되는 entity로 해석할 수 있다. 따라서 같은 entity라도 subject에서의 임베딩은 object에서의 임베딩의 켤레이다.
마지막으로 모델의 학습력을 Low-rank decomposition을 통해 정당화한다.
현재 우리가 이진 관계(기존의 $Y$행렬을 떠올려보자)를 다루고 있기 때문에 그 행렬이 low sign-rank를 갖고 있다고 전제한다. Sign-rank는 같은 sign pattern을 갖고 있는 모든 실행렬 중에서 가장 작은 rank를 의미한다.
Sign rank가 중요한 이유는 $Y$가 얼마나 복잡한 관계의 데이터인지 판단하는 기준이 되고(Linial et al., 2007) 이것이 모델의 학습력과도 연관이 있다고 밝혀졌기 때문이다(Alon et al., 2015).
이 가정을 통해 우리가 얻을 수 있는 것은 $Y$와 같은 sign pattern을 갖는 $X$(6)가 반드시 존재하며 $\textbf{E}\textbf{W}\bar{\textbf{E}}^T$의 rank는 $Y$의 sign rank의 2배가 최대이다(Trouillon et al.,2016). 주로 sign rank는 해당 행렬의 rank보다 많이 작다는 것을 감안하면 우리가 구하고자 하는 $X$의 학습력은 높다고 할 수 있다.
따라서 $\textbf{E}\textbf{W}\bar{\textbf{E}}^T$의 rank를 $K<<n$이라고 할 수 있고 diag(W)의 첫 $K$요소들만 non zero이므로 $\textbf{E}\in \mathbb{C}^{n\times K},\textbf{W}\in \mathbb{C}^{K\times K}$로 표현할 수 있는 것이다.
개별적인 두 entity에 대해 score를 표현하자면 아래와 같이 최종적으로 나타낼 수 있는 것이다.
$$\textbf{X}_{so}=Re\left ( e_s^T \textbf{W}\bar{e}_o \right )\cdots (7)$$
Architecture
이제 1개의 relation에 국한되지 말고 KB에 있는 모든 relation으로 확장해 보자. 일반적으로 $r$ 을 relation, $s$와 $o$를 각각 subject, object로 본다면 다음과 같이 일반화할 수 있다.
$$P(\textbf{Y}_{rso})=\sigma \left ( \phi \left ( r,s,o;\Theta \right ) \right )$$
triple $r(s,o)$에 대한 scoring function $\phi$과 해당 모델의 파라미터 $\Theta$로 구성됐다.
Scoring function에 대한 정의는 우리가 위의 섹션에서 살펴봤던 결과들을 토대로 다음과 같이 정의할 수 있다.
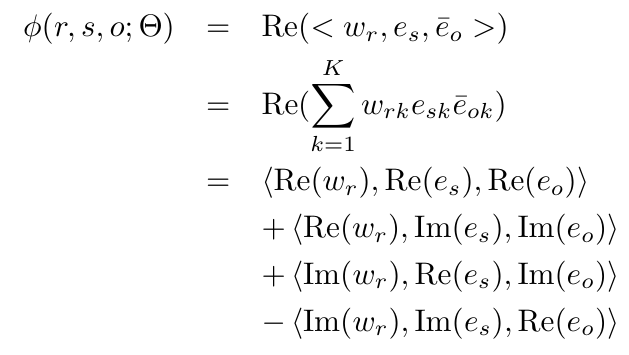
수학적으로 삼중 dot product는 정의되지 않았기 때문에 $<a,b,c>:=\Sigma_ka_kb_kc_k$와 같이 정의한다.
(부호들이 왜 저런지에 대해 간략히 설명하자면, $Im(v)$는 v벡터의 허수 부분이다, 즉 허수가 포함되어 있지 않다. 또한 $e_o$는 conjugate 된 상태임을 잊지 말아라! 따라서 $Im(\bar{e_o})=-Im(e_o)임을 감안하면 부호에 관한 오해가 풀릴 것이다.$)
Scoring function은 허수부 덕분에 antisymmetric 한 결과를 얻을 수 있다. 왜냐하면 이제 $<a,b,c>$와 $<c,b,a>$는
또한 $w_r\in \mathbb{C}^K$벡터와 함께 흥미로운 사실 두 가지를 도출할 수 있다.
1. $w_r$이 실수이면 scoring function은 symmetric하다.
$$\phi=<Re(w_r),Re(e_s),Re(e_o)>+<Re(w_r),Im(e_s),Im(e_o)>$$
$w_r$이 실수 벡터로 정의되어 있으면 DistMult와 거의 흡사한데, 이는 DistMult가 왜 symmetric relaiton만 학습할 수 있었는지 알려주는데, $<r,s,o>=<r,o,s>$를 반드시 만족하기 때문이다.
2. $w_r$가 순허수이면 scoring function은 antisymmetric 하다.
$$\phi=<Im(w_r),Re(e_s),Im(e_o)>-<Im(w_r),Im(e_s),Re(e_o)>$$
DistMult에서는 찾아볼 수 없는 특성인 이유는 복소 공간으로 확장하지 않았기 때문이다. 따라서 $<r,s,o>=-<r,o,s>$를 반드시 만족한다.
Experiments
Symmetric과 antisymmetric relation에 효과적인 모델링이 가능한지 알아보기 위해 한쪽은 완전히 symmetric, 다른 쪽은 완전히 antisymmetric 한 relation으로 채워진 $2\times30\times30$크기의 tensor를 학습시킨다.
Symmetric 데이터는 대각을 기준으로 빠진 데이터 제외 전부 색이 일치하지만 antisymmetric은 전부 색이 반대이다.
실험 결과를 보기 전에 측정 지표는 MRR과 Hits at m을 사용한다.
이에 대한 결과를 보면 ComplEx가 가장 좋은 성능을 보임을 알 수 있다.
주성분 분석(PCA)을 사용해 시각적으로 봐도 DistMult는 antisymmetric relation을 비슷한 위치에 임베딩 시켰고(_part_of, _has_part) ComplEx는 거의 대칭되게 학습시켰음을 알 수 있다.
Conclusion
Antisymmetric relation까지 학습가능한 모델을 제시하였다. 또한 모델의 성립 과정에서 수학적인 정당성을 갖고 가 이론적으로나 실제 성능적인 측면에서나 둘 다 우수한 모델이며 이 과정에서 과거 모델인 DistMult의 한계점도 수학적으로 증명하였다.
