Paper :
Main Interest
지식 그래프(Knowledge Graph ; KG)는 노드와 노드 간의 연결을 간선에 저장한다. 기존의 그래프와의 차이점은 간선이 오직 방향성(in, out, undirected) 뿐만 아니라 간선의 종류(relation)에 의존한다는 것이다. 즉 데이터는 triplet 꼴로 저장이 되는데, 예시로 (Obama, born in, Hawai), (Hawai, state of, USA)이 있다.
이러한 지식 데이터(Knowledge Base ; KB)를 모델에 학습시켜 추천 시스템부터 시작해 사실 확인, 검색 엔진, NLP 등 여러 분야에서 사용할 수 있다. 그렇다면 모델 학습은 어떻게 시켜야 할까?
KB를 효율적이게 학습하고자 여러 시도들이 있었고 그중 가장 인기 있는 접근은 tensor factorization과 neural-embedding-based model이다. 이 둘은 방법론적인 차이가 있지만 entity(노드;Obama)와 relation(간선;born in)의 저차원 임베딩으로의 인코딩을 목표로 한다는 공통점이 있다. 또한 KB 학습에 있어서 유의해야 할 점은 데이터의 크기가 매우 크다는 것이다. Bench mark dataset 중 하나인 FreeBase의 경우 100만 개 규모의 entity와 10억 개 규모의 triplet이 존재한다. 즉 모델들은 반드시 연산 효율적이고 큰 KB로도 확장 가능해야 한다.

기존의 성능이 뛰어나다고 평가된 TransE와 NTN은 neural-embedding model이고 tensor factorization 기반이었던 RESCAL에 비해 고성능을 보여주었기 때문에 DistMult는 energy-based neural networks를 사용한 neural-embedding model을 따른다.
Problems with previous works
일단 DistMult는 link prediction과 rule mining에서 높은 성능을 보인다. Link prediction에 대해서 고안된 모델들 중에서 대표적인 것이 TransE와 NTN이 있는데, TransE는 entity와 relation을 단일 벡터로 임베딩하여 $\textbf{h}+\textbf{r}\approx \textbf{t}$의 관계를 만족하도록 학습하고 NTN은 두 entity의 관계를 bilinear tensor operator와 linear matrix operator, 두 부분으로 나누어 계산한다. TransE의 가벼운 연산 덕분에 당시에 가장 좋은 모델로 평가받았지만 대칭 관계(symmetric relation;(A, friend with, B), (B, friend with, A))를 학습할 수 없다는 문제점이 있었다.
반면에 rule mining의 경우 RecNN에서 parse tree에 기반한 단어의 특성으로 neural network를 이용해 논리 결합과 부정을 학습할 수 있었다. 더 나아가서 RecNN을 활용해 수량사(some, all)를 포함한 추론에 활용할 수 있었고 임베딩 값에 근거한 지도 학습으로까지 발전하게 되었다. 하지만 기존의 연구들은 적은 양의 데이터와 제한된 논리 형식에서만 학습이 일어났다는 한계점이 있다.
이런 한계점들을 극복하여 symmetric relation도 학습 가능하고 rule mining에서도 scalability와 generalizability를DistMult로 동시에 얻을 수 있음을 피력한다.
Architecture of DistMult
DistMult는 neural network 기반 framework이다. 정확한 구조를 살펴보기 전에 데이터가 어떻게 담겨 있는지 설명하자면, KB가 주어졌을 때 어떤 1개의 관계를 표현할 때 $(e_1, r, e_2)$로 표현한다(각각 subject, relation, object를 한다 ; subject -> relation -> object).
Scoring
전체적인 구조는 2 layer neural network이고 첫 번째 층에서 input entity 쌍을 저차원으로 임베딩하고 두 번째 layer에서는 앞에서 받은 두 벡터를 갖고 특정 relation(relation의 종류에 따라 다른 파라미터 행렬 또는 벡터를 이) 파라미터에 대해 scoring을 실행한다.
$e_1$을 표현하는 벡터를 $\textbf{x}_{e_1}$, $e_2$를 표현하는 벡터를 $\textbf{x}_{e_2}$로 표현하고 이 벡터들을 갖고 first layer에 projection 해주면 각 entity에 해당하는 임베딩 벡터($\textbf{y}_{e_1}$, $\textbf{y}_{e_2}$)가 나온다.

$f$는 선형 또는 비선형 함수일 수 있고, $\textbf{W}$는 미리 학습된 파라미터 행렬이거나 무작위로 초기화된 행렬일 수 있다.
자, 이제 두 개의 임베딩 entity 벡터를 얻었다. 이제 우리가 정의할 것은 relation을 어떤 방식으로 entity 벡터들과 엮어줄 것이냐 이다. 엮는 방식에 따라 score이 신뢰할 수 있는지 없는지 나오게 되기 때문에 사실상 relation과 entity 사이의 관계를 정의하는 것이 이 모델의 핵심이라고 할 수 있다.
이 논문에서는 기존의 여러 대표적인 모델들이 이 단계에서 취한 scoring function을 나열하였다. 기호들의 자세한 의미는 논문에서 확인해 주기를 바란다.

필자는 NTN에 대해 linear, bilinear relation operator을 모두 사용한 모델이기 때문에 가장 expressive 하다고 평가하였고 TransE의 경우 벡터 연산 덕부에 가장 가볍고 단순한 모델이라고 평가하였다. DistMult는 이 두 모델의 장점을 1개씩 끌어오고자 한다.
DistMult에서는 bilinear transformation에 기반한 scoring function을 선택하였다.

이는 NTN 모델의 특수한 경우인데, 왜냐하면 NTN의 경우 linear과 bilinear의 합을 사용하 반면 DistMult에서는 bilinear만 사용하자고 제안한다. NTN과 또 다른 점은 $\textbf{M}_r$의 모양에 있다. NTN의 경우 $\mathbb{R}^{n\times n\times m}$크기의 텐서($n\times n$ 크기의 행렬층 $m$개)를 사용하였지만 이를 단순화시켜 DistMult에서는 파라미터의 개수를 줄이고자 $\textbf{M}_r$을 대각 행렬($\mathbb{R}^{n\times n}$)로 제한한다. 이는 결국 TransE와 같은 개수의 relation 파라미터를 요구하게 되는 것이다.
이를 단순화한 표현으로 $S(e_1,r,e_2)$ 으로 score를 나타낸다.

정리하자면 DistMult는 NTN의 복잡성(bilinear)과 TransE의 단순성(적은 개수의 파라미터)을 결합한 모델이라고 할 수 있다.
참고로 $\textbf{y}_{e_1}$, $r$,$\textbf{y}_{e_2}$ 3개의 벡터 간의 dot product라고도 해석할 수 있다.
Loss
Positive sample과 negative sample을 활용해 손실 함수를 구성한다. Negative sample은 relation은 내버려두고 entity 2개 중 1개만 바꾸어 마치 기존의 데이터를 손상시켰다고 하여 corrupted triplet이라고 한다. 단, 이렇게 만들어진 corrupted triplet은 기존의 positive sample($T$)에 있지 않도록 한다. 양쪽 다 바꾸지 않는 것에 대한 설명은 이 글의 appendix에 남긴다.

위의 loss는 margin-based ranking loss이다. Positive triplet의 점수가 negative보다 margin(여기서는 1) 만큼 크면 loss를 0으로 설정해 준다.
Experiments
1. Link prediction
모든 entity 임베딩 벡터에 renormalization(standard L2 regularization)을 계속해주면서 unit 크기를 만족시키도록 한다. 이 방법은 모든 모델들에 대해서 경험적으로 좋은 성능을 내는 데에 사용된 방법이다.
평가 방법으로는 MRR(Mean-Reciprocal Rank), Hits@10(top 10 accuracy)를 이용한다. 두 수치 모두 클수록 좋다.

Bilinear-diag가 이 논문에서 제시하는 DistMult 모델이다. 여기서 TransE를 DistAdd라고 명명하였는데 그 이유는 사실 TransE는 $\mathbf{h}+\textbf{r}\approx \textbf{t}$를 사용하고 DistMult는 $\mathbf{h}\cdot \textbf{r}\cdot \textbf{t}$를 사용하기 때문이다.
또한 논문에서는 WN에서 특히 Bilinear model이 TransE를 압도한다고 하는데 그 이유를 WN에 entity의 개수가 많고 그만큼 다양한 relation을 학습하기에는 모델의 bilinear성이 linear보다 더 다양한 특징들을 파악할 수 있기 때문이라고 설명한다.

2. Rule extraction
Warning : DistMult의 composition 학습력은 가정 1개에 무겁게 의존하기 때문에 composition이 불가하다고 평가된다. 그 가정은 appendix에서 설명한다.
전통적인 rule mining 기법들은 scalability 문제가 많았다. 따라서 DistMult를 활용한 KB의 규모가 아닌 relation의 종류에 영향을 받는 모델을 제안한다. Relation의 개수는 KB의 전체 규모에 비하면 상대적으로 매우 작고 실험 결과에 의하면 강한 일반화 모델임을 증명해주고 있기 때문에 효율적인 모델임을 알 수 있다.
KB로부터 논리적 규칙들을 학습하는 것을 목표로 한다. 아래와 같은 예시처럼 $r_1,r_2$를 통해 $r_3$를 추론하는 것이다.

이러한 작업은 4 가지의 장점이 있다.
1. 새로운 사실을 추론해 내는 데에 도움을 줄 수 있다.
2. Rule만 저장하고 이후 추론이 필요할 때만 정보를 만들어냄으로써 거대한 양의 추가 공간 없이 데이터 저장을 최적화할 수 있다.
3. 복잡한 추리를 도와줄 수 있다.
4. 추론 결과를 설명해 줄 수 있다(추론에 사용된 entity들과 relation들을 보면 된다).
- Background
우리의 목적은 Horn rule을 추출하고자 한다.

여기서 $a_i$는 entity가 들어갈 수 있는 변수를 지칭하고 $B_k(a_i, a_{i+1})$은 하나의 triplet을 의미한다. 결국 우리가 포착하고자 하는 것을 그림으로 그리면 다음과 같다.

Horn rule을 추출하고자 할 때 $r$과 이의 inverse relation 인 $r^{-1}$이 존재하면 다음과 같은 규칙성도 있다.

우리는 서로 다른 relation에 대한 rule mining을 하고 싶기 때문에 $B_1,...,B_n,H$가 서로 별개의 relation으로 한정한다.
Rule은 모든 변수가 entity로 대체되면 인스턴스화(instantiated)된다. 구체적인 법칙으로 자리 잡았다고 생각하면 편할 듯하다. 또한 기하급수적으로 증가하는 탐색 범위를 줄이기 위해 rule length를 2, 3으로 제한한다(rule length 1은 일반 triplet을 의미함).
마지막으로 어떤 relation들은 특정 종류의 entity만을 인수로 가질 수 있다. 예를 들어 $\textit{BornInCity}$는 사람을 subject, 위치를 object로 가져야 한다. 따라서 relation $r$에 대해 subject의 domain을 $X_r$, object의 domain을 $Y_r$으로 명명한다. 이렇게 domain을 한정하는 것은 탐색 범위를 줄이는 데에 매우 효과적이다.
- Rule extraction
단순성을 위해 length가 2인 경우만 살펴보자.

수식 1을 어떻게 모델이 학습하게끔 유도할 수 있을까? 생각보다 단순한 게
$\textbf{y}_a^T\textbf{M}_1\approx \textbf{y}_b^T$, $\textbf{y}_b^T\textbf{M}_2\approx \textbf{y}_c^T$를 동시에 만족하면 $\textbf{y}_a^T(\textbf{M}_1\textbf{M}_2)\approx \textbf{y}_c^T$를 함축하고 있는 것과 다름없다. 자세한 증명과 이유는 appendix에 남긴다.
수식 1의 개연성을 위해 $B_1$과 $B_2$의 관계 구성은 $H$와 비슷한 임베딩을 갖고 있어야 한다. 본 논문에서 가정하기로는 임베딩 행렬 간의 유사도는 Frobenius norm으로 측정할 수 있다.
하지만 의문이 드는 게 너무 많은 양의 triplet을 샘플링해야 하지 않나 생각이 들 수도 있다.

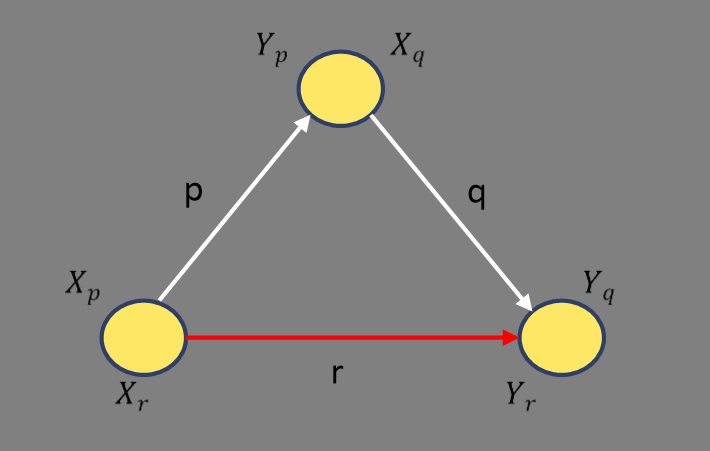
다행히도 위의 수식처럼 어떤 relation $r$에 대해 rule을 학습하고 싶으면 relation $p,q$에 대해 위 수식을 전부 만족하는 entity domain만 찾아보면 된다.

특정 $r$에 대해서 S집합과 T집합을 선택하고 가능한 모든 relation sequence를 모은다(아마 수식 2를 만족하는). 이후에 K-nearest neighbor(K-NN)으로 relation sequence(예를 들면 {$pq$, $p^{-1}r$})와 $\textbf{M}_r$ 사이의 distance(Frobenius norm)를 측정하여 $\textbf{M}_r$과 가장 근접한 relation sequence를 $\delta$(heuristic threshold)만큼 rule로 인정해 주고 $Q$에 추가해 준다.


결과를 보면 이 연구에서 제시한 Bilinear과 DistMult 계열의 모델들이 좋은 성능을 보이고 있음을 알 수 있다.
Length = 2에서는 기존의 가장 강력했던 AMIE모델과 비교했을 때도 DistMult는 좋은 성능을 보여주었다.
Conclusion
DistMult는 기존의 강력했던 TransE와 NTN의 장점들을 통합한 모델이라고 할 수 있다. Entity와 relation 사이의 bilinear 관계를 사용해 더 다양한 표현력을 KB에서 포착할 수 있게 되었으며 파라미터의 개수를 TransE의 수준까지 낮추어 matrix multiplication을 사용함에도 불구하고 light 한 모델을 고안하였음에 의의가 있다. 또한 rule mining에서도 좋은 성능을 보여주어 지식 그래프에서의 task를 다양하게 적용할 수 있는 모델이다.
하지만 DistMult의 경우 antisymmetric($h$와 $t$의 위치가 바뀌어도 score이 같음), inverse(두 relation matrix가 동치이어야 함), composition relation(appendix에서 설명)을 학습할 수 없다는 단점이 있다.
Appendix
1. 수식 1의 행렬곱 증명

$\textbf{y}_a^T\textbf{M}_1\approx \textbf{y}_b^T$ (1)
$\textbf{y}_b^T\textbf{M}_2\approx \textbf{y}_c^T$ (2)
전제($\textbf{y}_s\textbf{M}_r\textbf{y}_o\approx 1$)에 따라 위의 두 식이 만족한다.
이제 위의 두 근사식이 유효할 때 $\textbf{M}_1\textbf{M}_2\approx \textbf{M}_r$을 만족하여 2개의 relation 곱이 length 2의 body rule로 표현되어 Horn rule($\textbf{M}_r$)을 도출할 수 있음을 보이겠다.
먼저 (1)과 (2)를 곱한다. 크기를 맞춰야 하기 때문에 (2)를 전치한 상태로 곱한다. Entity 임베딩($\textbf{y}$)은 벡터, $\textbf{M}$은 대각 행렬임을 기억하자.
$(\textbf{y}_a^T\textbf{M}_1)(\textbf{y}_b^T\textbf{M}_2)^T\approx \textbf{y}_b^T\textbf{y}_c$
좌변의 전치를 분배해 주고 우변에 전치를 해주면(벡터곱은 결과가 스칼라이므로 전치시켜도 값이 일정하다)
$\textbf{y}_a^T\textbf{M}_1 \textbf{M}_2^T\textbf{y}_b\approx \textbf{y}_c^T\textbf{y}_b$
대각 행렬은 전치를 해도 본인이므로
$\textbf{y}_a^T\textbf{M}_1 \textbf{M}_2\textbf{y}_b\approx \textbf{y}_c^T\textbf{y}_b$
정리해 주면
$\textbf{y}_a^T(\textbf{M}_1 \textbf{M}_2)\approx \textbf{y}_c^T$ (3)
이 결과와 우리의 relation $H$에 대해 $\textbf{y}_a^T\textbf{M}_r\approx \textbf{y}_c^T$을 만족하기 때문에
$\textbf{M}_1\textbf{M}_2\approx \textbf{M}_r$을 만족함이 증명되었다. 이는 length = 2 뿐만 아니라 어떤 길이의 rule이든 적용된다.
2. Antisymmetric relation, inverse relation 학습 불가
- Antisymmetric relation
비대칭 relation에 대해 (a, r, b)와 (b, r, a)에 대해 항상 같은 score를 갖는다. 왜냐하면 $(ABC)^T=C^TB^TA^T$이므로
$(\textbf{y}_a^T\textbf{M}_r\textbf{y}_b)^T=\textbf{y}_b^T\textbf{M}_r\textbf{y}_a$를 만족하기 때문이다.
- Inverse relation
즉 $(h, r1, t)$과 $(t, r2, h)$가 있다면 반드시 $r1=r2$를 의미한다. 위의 유도 과정을 그대로 갖고 오면 증명이 된다.
$(\textbf{y}_h^T\textbf{M}_{r1}\textbf{y}_t)^T=\textbf{y}_t^T\textbf{M}_{r1}\textbf{y}_h=\textbf{y}_t^T\textbf{M}_{r2}\textbf{y}_h$
$\therefore \textbf{M}_{r1}=\textbf{M}_{r2}$



