Paper :
Main interest
지식 그래프(Knowledge graph, KG)는 방대한 크기의 정보 담고 있으며 2개의 entity(h, t)와 1개의 relation(r)으로 하나의 triplet을 구성하고 이것이 KG의 데이터 단위가 된다. 예를 들어 $(h, r, t)$로 triplet을 표현할 수 있고 조금 더 relation 중심으로 표현하면 $r(h, t)$로 표기할 수 있다. 다만 주의해야 할 것은 일반적으로 $(h, r, t)$는 h->r->t를 의미하지만 이 연구에서는 $r(h, t)$를 더 많이 사용하고 t->h 방향으로 relation이 뻗어간다. 앞으로 글에서 $r(h, t)$를 표준으로 사용하겠다.
다양한 데이터를 담고 있는 만큼 지식 데이터(Knowledge base, KB)에서 규칙들을 추론할 수 있는데, 예를 들어 아래와 같은 규칙(rule)을 추론할 수 있다.
$X, Y, W$은 logical 변수이고 말 그대로 domain만 일치하는($parent(X,W)$에서 $X$는 반드시 사람이다) 어떤 entity가 들어와도 상관하지 않는 일반적인 규칙을 학습할 수 있다. 이것을 rule mining이라고 한다.
이러한 논리 규칙들을 학습하는 것은 KB에서 추론 작업을 함에 다음 이유들 때문에 굉장히 유용하다.
1. 해석 가능성 : 위의 rule mining 예시처럼 $uncle$을 표현하기 위해 $parent$와 $brother$이 rule의 body임을 알 수 있다. 즉 rule의 내부를 뜯어 해석할 수 있다.
2. 일반성 : 가족 관계가 아닌 다른 영역에 대한 KB일지라도 일정한 rule mining 알고리즘을 사용하면 relation들의 관계를 학습할 수 있기 때문에 타 분야 학습으로도 견고히 전환할 수 있다(robustness in transfer tasks).
위의 가족 관계 예시를 다시 갖고 와서 새로운 가족에 대한 데이터가 들어올지라도 일반적인(logical variable) 모델 덕분에 retraining 없이도 사용할 수 있다. 이는 특정 entity, relation의 임베딩을 학습하는 모델(e.g., TransE)과의 차이점이자 강점이 된다. 임베딩 모델들은 새로운 노드에 대한 임베딩을 생성하기 위해 학습을 다시 돌려야 하는 transductive 한 접근이기 때문이다.
Relation rule 학습은 statistical relational learning(SRL)이라고 할 수 있다. 이는 불확정적이고 복잡한 관계 기반의 구조를 학습하는 것을 의미하는데, 두 entity 사이의 빠진 link를 보강하는 link prediction task가 그중 하나이다. 이는 Markov Logic Networks, ProPPR과 같이 어떤 개체 간의 관계를 확률 기반으로 바라본다. 또한 relation rule 학습은 기존의 rule들을 이용해서 새로운 logical rule을 도출하기 때문에 inductive logic programming이라고도 할 수 있다. 여기서 inductive는 지도학습의 의미가 아니라 관측된 relation들을 기반으로 논리를 학습한다는 뜻으로 이해할 수 있다.
SRL 방식을 취하면서 노이즈 많고 복잡한 데이터에 대해 더 부드러운 학습을 할 수 있다. 즉 단순히 있다(1)와 없다(0)의 문제가 아닌 그 중간도 표현함으로써 표현 범위가 더 넓어진 것이다. 하지만 이는 상당히 중요한 문제점이 따르는데, 바로 KB의 rule의 구조(rule을 구성하는 body relation)와 파라미터(모델을 구성하는 가중치)를 동시에 학습할 수 있는 모델을 만들어야 하는 것이다. 구조를 결정하는 것은 순전히 이산적인 문제(rule을 구성함에 있어 어떤 relation이 있냐, 없냐의 문제)와 순전히 연속적인 문제(파라미터 값 결정은 실수 공간에서의 문제)를 동시에 해결해야 하는 것이다.
이런 문제점들을 극복하고자 Neural LP는 최초로 neural network를 활용한 미분 가능한 end-to-end 모델을 제안하였다. 결론적으로 이 연구에서는 rule mining을 통해 추론이 가능한 모델 구축을 목적으로 한다.
Problem with previous models
Rule mining을 위한 시도들은 다양하게 있는데 대표적으로 structure embedding과 discrete search가 있다.
Structure embedding은 KB의 entity와 relation을 텐서 또는 벡터로 임베딩해 임베딩 공간에서 관계를 학습한다는 특징이 있다. 이 방법은 entity와 relation이 기존 KB에서의 관계성을 잃지 않고 임베딩 되는 것을 목표로 하는 것이 logical rule을 학습하고자 하는 Neural LP와의 차이점이다. Structure embedding은 training에서 보이지 않은 entity나 relation 대해서 임베딩을 만들 수 없다는 한계가 있다.
조금 더 rule mining에 초점을 맞춘 알고리즘들이 선택한 방법은 problem space에서의 discrete search이다. MRC(Kok & Domingos, 2007)는 beam search(제한된 집합, 그래프에서 가장 유망한 노드로 뻗어가는 탐색법), Lao & Cohen(2010)은 제한된 집합에서 lasso-style 회귀를 사용해 예측한 rule들을 선택했다.
여기서 더 발전하여 neural programming에 기반한 induction 모델들이 제안되었는데 이들은 attention을 사용해 미분 가능한 연산자를 "부드럽게" 선택할 수 있게 하였다. 이 중 Neural LP에서 가장 큰 영향을 받은 것은 TensorLog의 연산자이다. 하지만 기존의 attention은 이진 선택의 정도 나타내는 척도일 뿐이었고 본 연구에서 attention은 logical rule에 대한 confidence(확신도)로 해석한다.
즉 Neural LP는 특정 rule로의 근사가 아닌 다양한 logical rule들의 확률적 분포를 학습한다.
Architecture
우리가 관심 갖는 task는 query를 포함한 것들이다(통상적으로 query는 relation과 entity를 가리키지만 여기서는 relations를 가리킨다). KB에서 추론을 학습하기 위해 아래와 같이 연쇄적인 logical rule의 가중치를 학습하며 이는 불확정적인 rule을 확률로 나타내기 때문에 stochastic logic program과 비슷한 맥락이다.
여기서 $\alpha \in [0,1]$는 이 rule($query(Y,X)$)의 confidence이고 $R_1,\cdots ,R_n$은 KB의 relation들이다. 이때 주어진 entity $x$에 대해 $y$의 적합도(score)는 $query(Y,X)$를 구성하는 rule들의 confidence 합이다.
대충 confidence에 대해 소개하였고 이제 본격적으로 Neural LP를 구성해 보도록 하겠다.
TensorLog operator
Neural LP의 기본 요소인 TensorLog operator에 대해 소개하겠다. KB에 대해 $\textbf E$를 전체 entity 집합, $\textbf R$을 전체 relation 집합이라고 하자. 이에 따라 모든 entity를 하나의 정수(i)에 대응시키면 entity를 $i$번째 원소만 1인 one-hot vector $\textbf{v}_i\in\left\{ 0,1\right\}^{|\textbf{E}|}$로 나타낼 수 있으며 각 relation $R$마다 operator $\textbf{M}_R$를 정의할 수 있게 된다. 이때 $\textbf{M}_R$는 $\left\{ 0,1\right\}^{|\textbf E|\times |\textbf E|}$의 모양을 갖고 $R(i,j)$을 만족할 때 $(i,j)=1$인 희소 행렬로 이해할 수 있다.
앞서 소개된 one-hot 벡터와 희소 인접 행렬을 이용해 추론 과정을 수식적으로 도출할 수 있는데 그 방법은 $\textbf{M}_P\cdot \textbf{M}_Q\cdot \textbf{v}_x\doteq \textbf{s}$이다. 예를 들어 아래와 같은 KB에서 이 수식을 적용해 본다고 하자.
위의 결과, (2,0,0,0) 벡터가 우리의 $s$가 되었는데, 이것은 entity 2를 시작으로 하고 $R_1 \to R_2$로 이어지는 경우의 수이다. (2,3,1)과 (2,4,1) 총 2개가 있음을 알 수 있고 이것이 $s$에 반영된다. 결국 우리는 $s$가 $y$집합과 일치하기를 바랄 뿐이다. 이는 rule의 길이가 2가 넘어갈 때도 적용 가능하다.
따라서 우리는 각 $query$마다 다음 수식을 학습하고 싶은 것이다.
$l$은 가능한 모든 rule을 인덱싱 하고(추상적인 의미가 많이 담겨있지만 간단하게 "모든 relation"이라고 이해해도 무방하다. 왜냐하면 rule과 relation은 사실상 같기 때문이다.) $\alpha_l$은 해당 rule $l$의 confidence이다. $\beta_l$은 $l$을 구성하는 relation의 순서이다(예를 들어 그림 1의 경우에 $\beta_l=[R_1,R_2]$). 추론 과정에서 벡터 $\textbf{v}_x$에 대해 다음과 같이 score를 정의할 수 있다.
예를 들어 특정 rule $l'$에 대해 body relation($\beta_l$)을 올바르게 구성했으면 벡터 $s$의 $y$번째 entry의 숫자와 유사할 것이다. 이를 모든 rule에 대해 똑같이 적용해 생각해 보면 rule에 대한 body relation을 잘 구성할수록 $\textbf{v}_y$에 가까워질 것이고 결국 score의 향상에 기여할 것이다. 따라서 아래와 같이 쓸 수 있다.
$\left\{ x,y\right\}$는 해당 $query$를 만족시키는 entity 쌍이고 $\left\{ \alpha_l,\beta_l\right\}$는 학습해나가야 할 것들이다.
Neural LP
TensorLog operator를 통해서 rule의 적합도를 어떻게 평가하는지 간단히 살펴보았다. 이제 이를 활용해서 Neural LP를 구축해 보자.
앞에서도 잠시 언급했듯이 우리는 결국 differentiable 한 모델을 만들고 싶다. 그래야 우리가 좋아하는 gradient based 최적화 알고리즘들을 사용할 수 있기 때문인데, 유일한 장애물은 여전히 이산적인 $\beta_l$ 때문이다. 이를 해결하고자 다음과 같이 식을 변형시킬 수 있다.
$T$는 rule의 길이이고 $k$는 하나의 정수로 표현된 모든 relation에 대해 개별 relation을 나타낸다. 즉 길이 $T$의 body length를 갖는 rule들을 모조리 계산해 버리자는 것이다. 이산 공간 문제를 해결하기 위해 공평하게(?) 모든 경우의 수를 다 보자는 것이다. $a_t^k$는 깊이 $t$에서 relation $k$가 얼마나 신뢰성 있는지(confidence)를 나타내는 파라미터이다. 여기서 "깊이"에 대해 "rule을 구성하는 relation들에 대해 t번째 relation에 대한 state"로 정의한다. 즉 그림 1에서 $T=2$일 것이고 $R_1$이 첫 번째, $R_2$가 두 번째기 때문에 $R_1$에 대한 파라미터는 $t=1$인 것이고 반대로 $R_2$는 $t=2$에 해당한다.
즉 위의 수식은 rule 하나에 weight를 할당한 것과 반대로 어떤 relation이 어떤 깊이에 출현하였냐에 따라 weight를 할당해 주어 모델이 더 다채로운 특성들을 학습할 수 있게 되었다. 하지만 여전히 문제인 것은 $T$가 고정이기 때문에 같은 길이의 rule만 학습할 수 있다는 한계가 있다. 따라서 Neural LP의 최종본을 위해 recurrent를 사용한다.
Recurrent formulation을 위해 auxiliary(보조) memory vector $\textbf{u}_t$를 정의한다. 초기 메모리는 tail entity 벡터로 초기화된다.
이후로는 일반적인 상황에 대한 처리가 보이는데, 파라미터의 새로운 역할들을 먼저 소개하겠다.
memory attention vector $\textbf{b}_t$는 명칭에서 유추할 수 있듯이 memory($\textbf{u}_t$)에 대한 가중치 벡터이다.
operator attention vector $\textbf{a}_t$는 TensorLog operator를 "부드럽게" 적용해 줄 수 있는 가중치 벡터이다.
위 벡터들은 깊이마다 존재한다는 점을 명심하기를 바란다. 이 파라미터들은 다음과 같이 사용된다.
식이 상당히 난해하다. 예시를 살펴보며 이해해 보자.
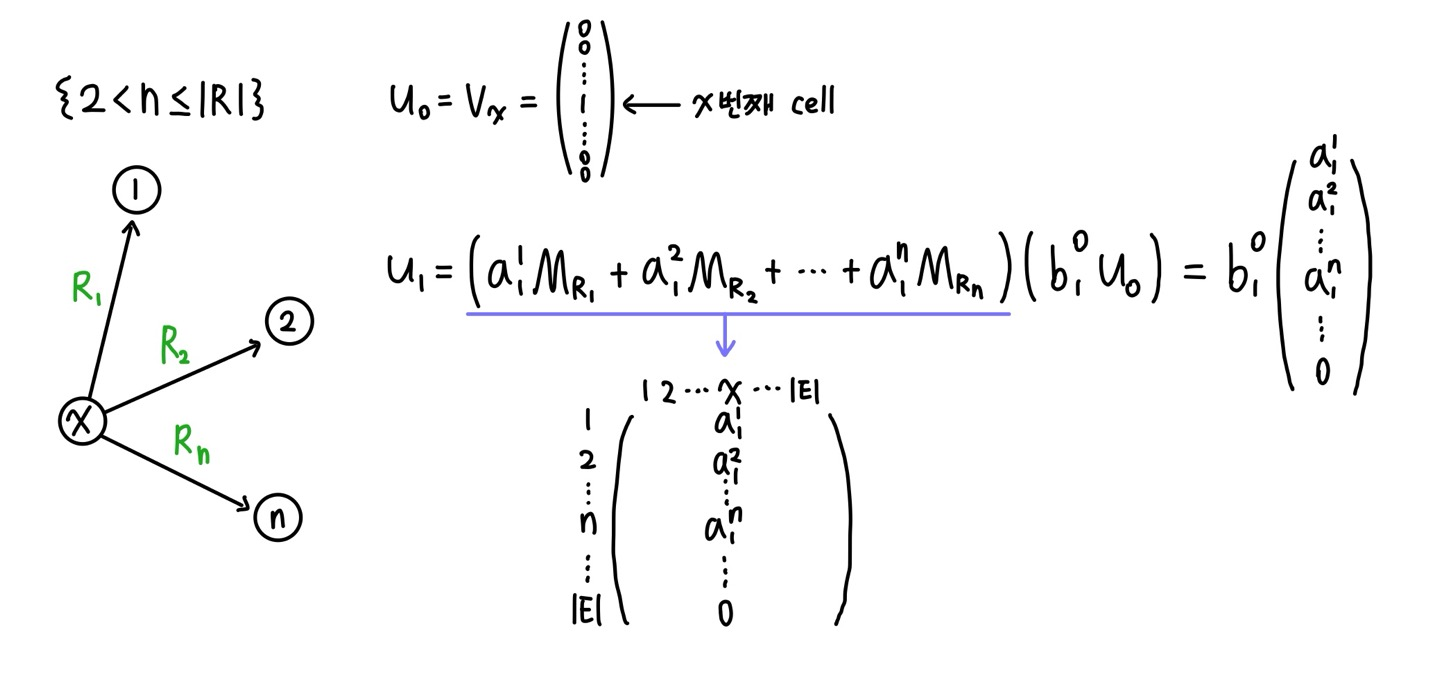
일단 깊이 1만큼의 rule을 mining 한 상태로 해석할 수 있다. 여기서 $\textbf{u}_1$은 보조 메모리이므로 1번째, 2번째, n 번째 cell만 값이 채워진 $\mathbb{R}^{|\textbf{E}|}$크기의 벡터로 저장된다. 행렬 계산에서 x열만 적은 이유는 어차피 $\textbf{u}_1$에서 x행만 1이기 때문이다. 한 단계만 더 깊이 들어가 보자.
A : 사실 깊이를 얼마나 깊게 가든 이 부분의 결과물들의 특정 cell의 값 존재 여부는 전부 같다. 여기서 유일한 변수(파라미터)는 operator attention vector이기 때문이다.
B : 사실 A와 함께 의미를 만들어나갈 수 있는 부분이다. $\textbf{u}_1$부분을 A와 곱해주면 1번, 2번, n번 노드에서 연결되어 있는 entity(몇 번 entity로 건너갔는가?), relation(몇 번 relation을 타고 넘어갔는가?)에 대한 정보들을 갖게 된다. 하지만 $b_2^0\textbf{u}_0$는 왜 필요할까? 그 이유는 엄연히 rule mining에서 순서는 매우 중요한 요소로 작용하기 때문이다. RNN에서 자연어 문장을 훑을 때 t번째 단어에 대해 propagate 하고 있음에도 이전 state들(1번째 단어, 2번째 단어,...)을 계속 저장하는 이유도 이와 같다. "깊이 t만큼 왔을 때 이전 state들을 얼마나 기억해야 하는가"를 나타내는 척도가 $\textbf{b}_t$인 것이다. 즉 현재 state(깊이)의 attention은 과거 state의 정보들에 의존한다.
마지막으로 과거의 모든 state들을 모두 모아 한번 더 attention과 계산해준다.
rule의 길이는 최대 T로 이미 끝난 거 아닌가?라고 생각할 수 있지만 $\textbf{v}_x,\textbf{v}_y$를 알고 있는 상태에서 무엇이 최적의 rule length인가를 알 수 있는 방법이 위의 수식이다. 즉 $\textbf{u}=\textbf{u}_{T+1}$와 $\textbf{v}_y$의 내적 결과를 maximizing 되는 방향으로 어차피 학습이 될 것이기 때문에 최적의 길이를 찾고 싶으면 $b_{T+1}^\tau$를 비교해 보면 된다. 여기서도 마찬가지로 "$\textbf{v}_y$와의 유사도 비교에 있어 $\textbf{u}_\tau$가 얼마나 큰 역할을 하는지"로 이해할 수 있다.
이 알고리즘을 기반으로 rule은 $(\alpha,\beta)$꼴로 confidence와 body relation이 한 번에 저장되는 것이다. 저장된 데이터에 대한 예시는 experiments에서 다루도록 하겠다.
Experiments
실험은 네 파트로 나뉜다. 각각에 대해 알아보기 전에 본 연구에서 KB를 3개의 file로 나누는데, 각각 facts, train, test로 나눈다.
facts : TensorLog operators $\left\{ \textbf{M}_{R_k}|R_k\in\textbf{R}\right\}$생성을 위해
train, test : query(head, tail) 데이터로 구성됨
임베딩 학습법과 달리 우리는 train에서 보인 entity와 test에도 존재할 필요가 없다.
Statistical relaiton learning
UMLS(Unified Medical Language System), Kinship(kinship relationships among members of the Alyawarra tribe from Central Australia)에 대해 실험을 진행한다. Dataset split ratio는 6:2:1이며 Hits@10에 대해 평가가 진행되며 비교 모델은 Iterative Structural Gradient(ISG, 2014)이다.
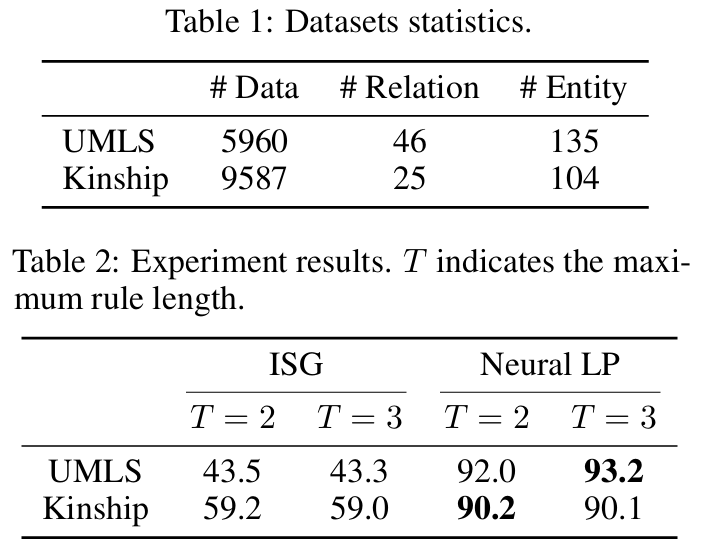
Grid path finding
위에서는 최대 깊이 3에 대해 학습을 시켰다면 이제 더 깊은 rule mining을 시도하기 위해 16*16 grid에서의 path finding을 KB로 가정하자. 여기서 relation은 방향(North, SouthEast)이고 entity는 좌표((1,2), (3,4))로 표현되며 하나의 데이터는 North((1,2), (1,1))와 같이 나타내진다. 이때 query는 랜덤으로 방향을 연속적으로 구성해(North_SouthWest) 생성한다. query를 2~10인 path length(start에서 finish까지의 hamming distance)에 따라 4개의 클래스(2-4, 4-6, 6-8, 8-10)로 나눈다.
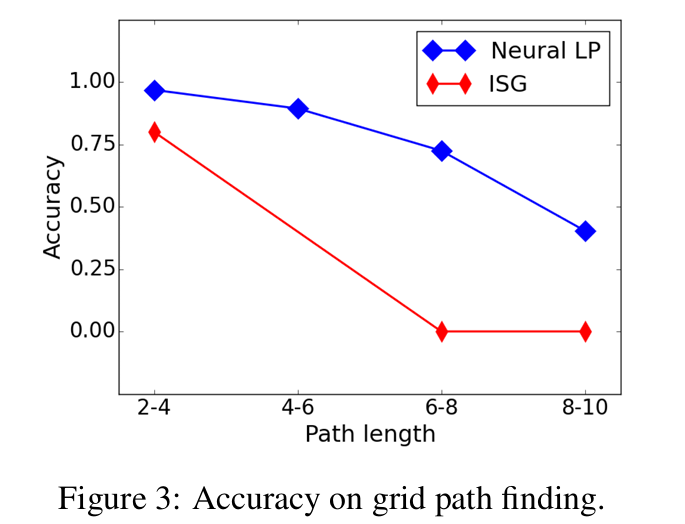
Knowledge base completion
query(head, tail)에 대해 query와 tail이 주어졌을 때 빠져있는 head를 유추하는 작업이다. 이때 우리의 neural network 모델을 위해 query를 차원 128의 임베딩 벡터로 나타내고 학습한다.
Completion에 대해 압도적인 성능을 보이지는 않지만 rule mining을 목적으로 개발된 모델치고 좋은 성능을 보인다고 할 수 있다.
Neural LP가 inductive learning에서 강세를 보임을 증명하기 위해 training과 testing에서 entity가 서로 겹치지 않게 데이터를 split 하고 completion task를 진행한다.
임베딩 기반 모델인 TransE는 사용 불가능한 수준으로 전락함을 볼 수 있다.
여기서 잠시 Neural LP에서 학습한 rule들의 형태를 살펴보자. 총 두 부분으로 나뉘는데, 좌측은 confidence, 우측은 rule은 구성이다.
Question answering on knowledge base
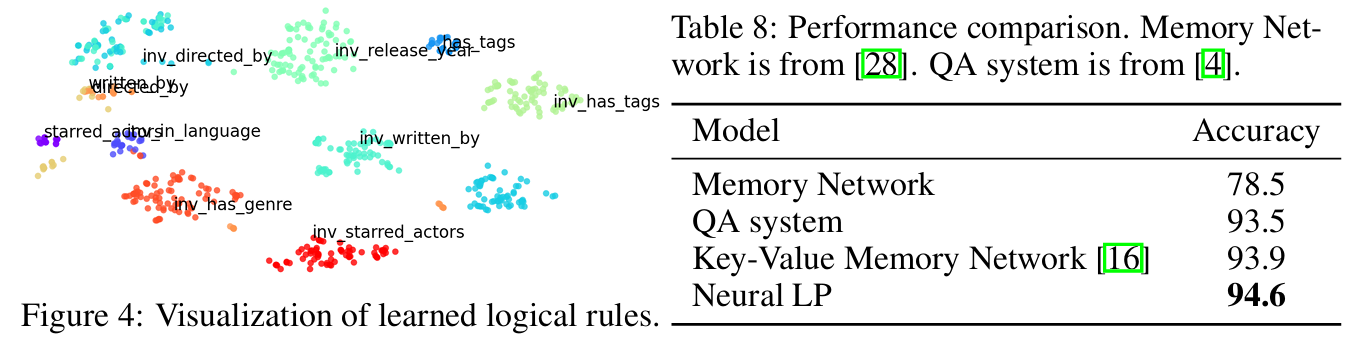
Conclusion
Rule mining 모델 중 최초의 end-to-end 미분 가능한 모델이다. KB의 학습에 있어 이산성과 연속성을 같은 공간 안에서 처리함에 의의가 있다.
