Paper :
Main interest
지식 그래프(Knowledge Graph, KG)는 그래프 형태의 데이터 구조이다. 간선의 종류가 제한된 일반적인 그래프와는 다르게 지식 그래프는 간선을 relation, 노드를 entity라고 부르며 이들의 연결(i.e. triplet $(h, r, t)$=$r(h,t)$)을 하나의 데이터 단위로 갖는다. 즉 아래의 그림과 같이 지식(Knowledge)을 통해 entity 사이의 관계를 그래프(Graph)처럼 표현할 수 있는 것이 KG가 된다.

KG인 데이터를 KB(Knowledge Base)라고 하는데 실세계 정보를 담아야 하는 만큼 KB의 규모는 매우 크다. 그만큼 모든 정보를 우리가 다 수집할 수 없기 때문에 KB는 주로 incomplete 하다. 따라서 우리의 주 관심사는 주어진 데이터에 한해서 빠져 있는 사실들을 추론하는 것이며 이를 KG reasoning이라고 한다. 즉 우리의 보편적인 목적은 testing에서 $(h, r, t)$가 주어졌을 때 $h$와 $r$만 갖고 $t$를 추론할 수 있냐이다.
Problem with previous models
$t$를 추론하기 위해 가장 활발히 연구된 방향이 두 가지 있다.
첫 번째는 entity와 relation을 latent space로 임베딩해 각 대상의 관계를 학습, 관찰하는 representation learning이다. 대표적으로 TransE(2014), DistMult(2014), RotatE(2019)가 있다. 이 방법의 장점은 주어진 triple 1개에 대해 일방적으로 학습하기 때문에 모델 구축에 있어 고려해야할 수고가 덜어지며 "임베딩이 어차피 latent space로 모델에 기인해 알아서 최적의 상태로 mapping 된다"라는 전제가 있기 때문에 임베딩 자체의 quality에 신경 쓸 필요도 없다. 하지만 transductive 하고 결과들이 해석 가능하지 않다는 한계가 있다. 먼저 transductive 한 이유에 대해 설명하자면, 예를 들어 training에 존재하지 않는 entity가 test에 존재하면 그 entity에 대한 test 자체가 불가능하다. 왜냐하면 임베딩 구축은 모델의 training 과정에서 생성되기 때문이다. 물론 모든 임베딩 기반 모델들이 transductive 한 것은 아니다. 대표적으로 GraphSAGE는 노드를 임베딩함에 있어 필요한 weight와 aggregator를 학습 후 저장함으로써 inductive 환경으로 끌고 온 바 있다. 하지만 이 방법은 애초에 KG에서 연구된 모델도 아닐뿐더러 message passing으로 노드를 임베딩하는 데에는 효과적일지 몰라도 relation에 대해서는 적용이 어려움이 있기 때문에 여전히 KG에서의 representation learning은 transductive 하다고 할 수 있다.
두 번째는 relation들의 조합들의 패턴을 학습해 추론을 하는 rule mining 기법이다. 가령 아래의 그림처럼 relation Appears_in_TV_Show를 rule들로 표현할 수 있다. 이 rule들을 통해 구하고자 하는 entity에 대한 정보를 rule로 우회해서 얻을 수 있는 것이다. 즉 $(h,r,?)$에 대해 $?$에 올 수 있는 entity의 확률을 구하여 rank를 매기는 방식으로 추론을 할 수 있는 것이다.

Rule mining의 장점은 transductive과 inductive setting 모두에 적용 가능하다는 것이다. 물론 완전히 자유로운 fully-inductive는 아니고 semi-inductive 정도의 성능을 보인다고 생각된다(구체적인 내용은 여기서). 따라서 rule mining이 representation learning 보다 근래에 더 활발히 연구되고 있다고 생각한다. Inductive setting이 중요한 이유는 KB는 날이갈수록 더욱이 거대해지고 있기 때문에(대략 100억 개의 triplet을 소유) transductive 방식대로라면 그렇게 거대한 데이터 전체를 매번 다시 학습하여 costly 하기 때문이다. 그렇다고 rule mining 모델들이 완전히 inductive하지는 않고 rule mining의 아이디어 자체가 같은 종류의 relation들만 담고 있는 KB에서 학습한 "rule"들을 갖고 추론을 할 수 있다는 관점에서 inductive 하다는 것이다.
Rule mining 접근들 중에 가장 대표적인 모델은 Neural LP(2017, NeurIPS)와 DRUM(2019, NeurIPS)이다. 이 둘은 공통적으로 rule을 구축하는 데에 있어서 이산성과 연속성을 동시에 해결해야 한다는 문제를 제기하고 이를 연속적인 공간으로 끌고 와 end-to-end differentiable 한 RNN 기반 모델을 구축함에 의의가 있다. 여기서 이산성이란 rule의 structure이고 연속성은 rule의 confidence이다.
Neural LP는 이 문제를 해결한 최초의 모델이며 DRUM은 이를 계승한 모델이라고 볼 수 있다. 하지만 이 방식은 매우 큰 search space를 요구하기 때문에 RNNLogic의 저자들은 이 문제에 대해 다른 접근법을 제안한다.
Architecture
방대한 search sapce 문제를 극복하기 위해 이들은 아래와 같은 방식을 제시한다.

쿼리 $\textbf{q}$는 하나의 triplet input 데이터이고 이 정보는 Rule Generator(이하 RG)에 들어가 $\textbf{q}$에 대한 rule의 다항 분포 $p_\theta (\textbf{z}|\textbf{q})$를 생성한다. 이를 통해 rule의 집합 $\hat{\textbf{z}}\subset\textbf{z}$을 뽑아내고 이를 Reasoning Predictor(이하 RP)로 전달해 $p_w(\textbf{a}|G,\textbf{q},\textbf{z})$를 생성해 주어진 그래프 $G$, 쿼리 $\textbf{q}$, $\textbf{z}$를 활용해 쿼리에 대한 예측 정답들($\textbf{a}$)을 뽑아낸다($\hat{\textbf{z}}$를 사용해야 하는 것 아니냐고 생각할 수 있지만 이에 대한 이유는 $\hat{\textbf{z}}$가 위 형식 제안 후에 간편성을 위해 제시된 것이기 때문이다). RG를 prior, RP를 likelihood로 취급하여 샘플링된 rule 중에서 가장 high-quality인 rule들을($\hat{\textbf{z}}_I$) 추린다. 그리고 이 결과를 이용해 RG를 업데이트한다. 학습은 이런 일련의 과정들로 이루어지며 testing에서는 RG 계산 이후 RP를 거쳐 바로 answer를 도출할 수 있게 된다. 이렇게 다른 sector에 다른 역할을 부여해준 것은 EM 알고리즘에서 영감을 얻었다고 하며 이 알고리즘이 확률 및 통계 값들을 활용하는 것을 RNNLogic에서 그대로 이어받았다.
주황색 과정이 E-step(Expectation), 초록색이 M-step(Maximization)이다.
즉 이 방법을 사용해 최적화시키면 이산성과 연속성을 별개의 문제로 취급해 처리할 수 있다.
일단 logic rule이 뭔지 정의하겠다. 어떤 triple을 다른 triple로 연속적으로 구성하는 것을 logic rule이라고 한다.

이때 $r$이 head relation이 되고 $X_i$가 head를 구성하는 body atom들이 되는 것이다. 이런 구조는 composition을 자연스럽게 포착할 수 있고 대표적이고 간단한 symmetric, inverse 등의 rule도 표현할 수 있다. 가령 $r^{-1}$을 $r$의 inverse relation이라고 한다면 symmetric rule은 아래와 같이 표현할 수 있다.
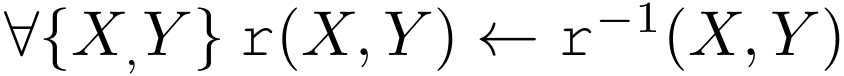
결국 우리가 구하고자 하는 가장 중요한 것이 rule이기 때문에 RNNLogic에서 rule을 latent variable(EM 알고리즘에서 영감)처럼 다룬다. 정확히 rule을 어떻게 생성하는지는 RG에서, rule의 평가는 RP에서 설명하겠다.
Probabilistic Formalization
어찌 되었든 우리는 optimization function이 필요하다. 이를 확률적으로 나타낼 수 있는데, RG $p_\theta$는 prior, RP $p_w$는 likelihood를 나타내기 때문에 이들을 합치면 아래와 같이 나타낼 수 있다.
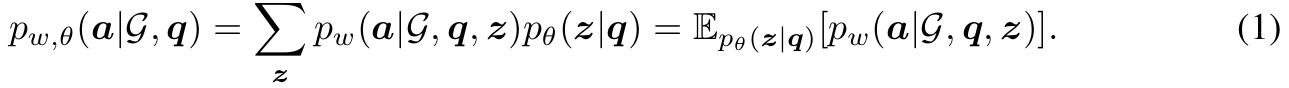
추상적인 대상에 대해 prior, likelihood로 명명하면 여간 헷갈리지 않을 수 없다. "확률"을 그 rule이 나타날 확률이 아니라 "신뢰도"로 이해하면 도움이 된다. 하지만 통계적 맥락을 위해 신뢰도 대신 확률로 계속 표현하겠다.

Prior($p_\theta(\textbf{z}|\textbf{q})$) :
"구하고자 하는 대상($\textbf{z}$) 자체의 확률"
RG에서는 $\textbf{q}$가 주어졌을 때 어떤 rule이 유망하고 어떤 rule이 유망하지 않은지 알 수 있게 해 준다.
Likelihood($p_w(\textbf{a}|G,\textbf{q},\textbf{z})$) :
"구하고자 하는 대상이 정해졌다고 가정할 때 주어진 대상($\textbf{a}$)이 나올 확률"
즉 $h$와 $r$와 이로부터 도출된 $\textbf{z}$를 토대로 $t$의 후보들을 확률적인 분포로 표현하는 것이다.
따라서 $p_\theta$는 분포적인 도구이고 실제 예측은 $p_w$로 이루어지기 때문에 likelihood의 최대화가 우리의 목적인 것이다. Log likelihood는 식조작에 편리하므로 사용해 준다.

Parameterization
<Rule Generator>
어떤 rule을 구성함에 있어 다음과 같이 표현할 수 있다.

여기서 $r$은 쿼리 $\textbf{q}$와 관련된 head relation이고 $r_i$는 body atom들, $r_{END}$는 relation의 연속의 끝을 표시하는 토큰으로 이해할 수 있다. 즉 우리는 $r$을 필두로 $r_i$를 구성하는 방법을 고안하면 되는데 이 문제에 대해서 RNN이 제격임을 알 수 있다. 이때 우리가 원하는 것은 $i$번째 relation의 후보군에 대한 확률 분포이다. 따라서 우리는 아래와 같이 RNN을 사용해 $p_\theta(\textbf{z}|\textbf{q})$를 표현하는 다항 분포를 얻을 수 있다.

$Mu$는 다항 분포를 뜻하며 $N$은 집합 $\textbf{z}$의 크기를 결정하는 하이퍼파라미터이고 $RNN_\theta(\cdot|r)$는 rule head가 $r$일때 각 깊이에서 body atom의 확률 분포를 정의하게 해 준다. 즉 아래와 같이 전체적인 구조를 나타낼 수 있는 것이다.
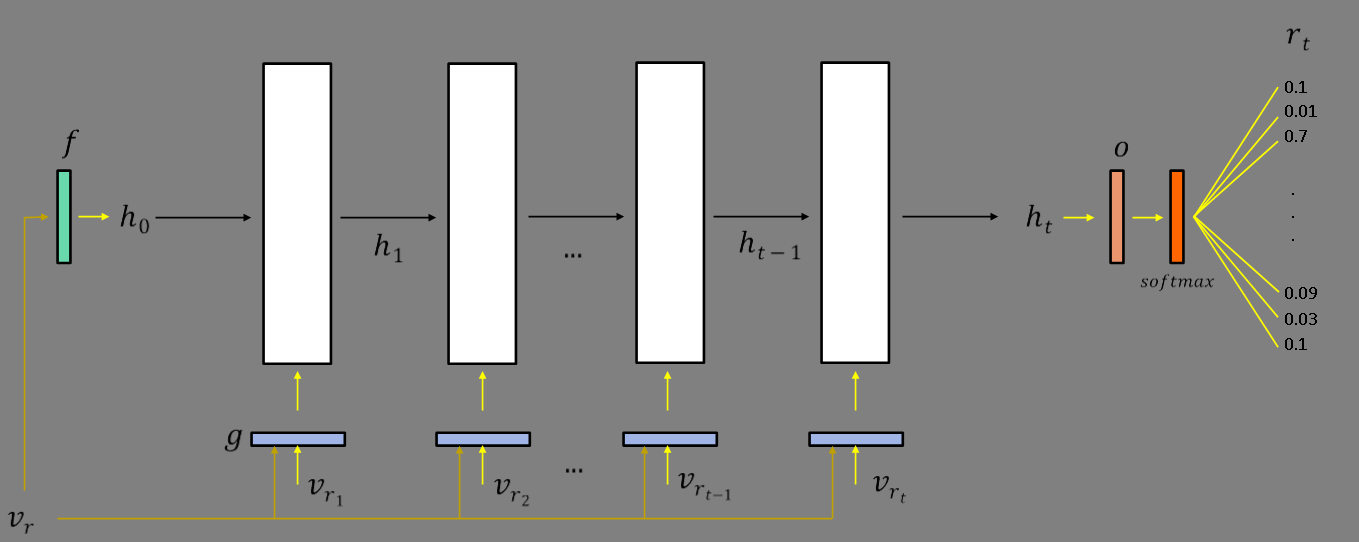
위 그림은 $[r,r_1,r_2\cdots r_t]$가 주어진 상태를 전제한 상황이다. 즉 과거의 state들을 갖고 다음 state를 도출하여 그에 상응하는 $r_{t}$의 확률 분포(relation 집합이 $R$이라면 $|R|$개의 relation에 대한 확률 분포를 생성)를 알아낼 수 있는 것이다. 여기서 드는 의문은 해당 깊이에서의 hidden state가 있어야 relation을 정할 수 있는데 정작 그 state를 구축하는 데에 그 relation에 대한 파라미터 벡터가 필요하다.

가장 그럴듯한 해석은 $v_{r_i}$는 $r_i$에 의존하는 파라미터 벡터가 아니라 깊이 $i$에 의존하는 벡터로 해석하는 것이다. 그래야지만 위의 의문이 해소되지만 정확한 방법은 논문에서 공개한 바 없다.
하지만 이 상태에서 어떻게 여러 rule들을 갖고 있는 $\textbf{z}$를 도출할 수 있을까? 이를 위해 모델은 beam search를 사용한다.

예를 들어 beam width가 2이고 $|R|=3$이라면 위와 같이 rule들을 수집할 수 있는 것이다. 특정 깊이에서 가장 확률이 높은 relation 2개를 선정해서 그 relation을 기준으로 $RNN_\theta$를 다시 돌려 다음 깊이의 확률 분포를 만든다.
즉 위의 간단한 예시에 의하면 $\left\{r_ar_ar_c,r_cr_br_b\right\}\in\textbf{z}$으로 샘플링할 수 있다. 따라서 $N$은 beam width임을 유추할 수 있다.
<Reasoning Predictor>
RG에서 받은 $\textbf{z}$를 이용해서 $p_w(\textbf{a}|G,\textbf{q},\textbf{z})$를 모델링하고자 한다. 주어진 쿼리 $\textbf{q}=(h,r,?)$에 대해 compositional rule과 $G$를 활용해 다른 candidate answer로 향하는 grounding path들을 찾을 수 있다. 즉 $\textbf{z}$와 BFS(또는 인접 행렬 이용, 이 부분은 논문에 나와있지는 않고 openreview에서 저자들이 밝혔다)를 사용해 이 정보들을 조합해 특정 candidate answer($e\in A$)에 대한 score를 얻을 수 있다.

$\psi_w(rule)$은 rule 자체에 대한 learnable 파라미터이고 $\phi_w(path)$는 경로에 대한 점수이다. 경로에 대한 점수는 1로 통일하는 방법과 RotatE를 사용하여 $h$를 시작으로 rule을 구성하는 body atom들에 상응해 임베딩을 움직였을 때 도착 지점이 $e$의 임베딩과 거리로 점수를 계산하는 방법이 있다. 이 두 가지 접근에 대한 성능은 experiments에서 비교된다. 여기서 매우 주의해야 될 점은 candidate answer들은 절대 $t$(정답 entity)와 가깝지 않다는 것을 전제로 한다. 이후에 나오게 될 모델의 구성에 대한 혼란을 피하기 위해 약간의 스포를 희생해 설명하겠다.
우리는 계산의 편리를 위해 $\textbf{z}$에서 $\hat{\textbf{z}}$을 샘플링 할 것이다. 더 나아가 $\hat{\textbf{z}}$에서 $K$개의 best high-quality rule $\hat{\textbf{z}}_I$을 뽑아내고자 한다. 하지만 candidate answer들은 우리가 인정한 최고의 rule을 통해 나온 것들이 아니다!! 따라서 $e\in A$가 어떤 집합에서 나왔는지에 대한 분포를 살펴보면 아래와 같을 것이다.
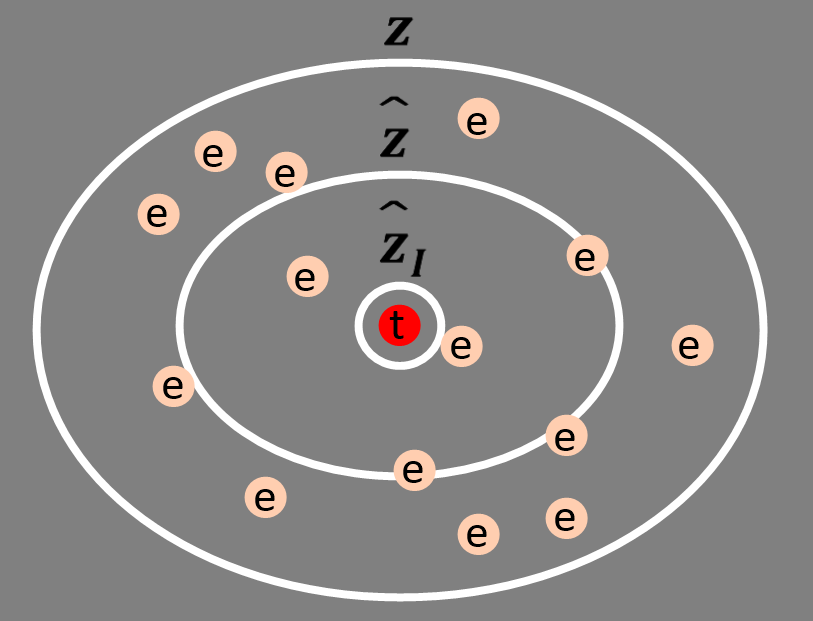
물론 $e=t$인 경우가 생길 수도 있지만 확률이 희박하며 만약 실제로 그런다고 해도 이후에 $\hat{\textbf{z}}$의 rule들로 $\hat{\textbf{z}}_I$를 뽑기 위한 최종 신뢰도를 평가하는 $H(rule)$를 보면 크게 상관없음을 알 수 있다.

이는 즉 어떤 rule에 대해 $t$는 positive example, $e$는 negative example 취급한다. 특히 negative example에 대해서는 평균을 내는데 이 안에 $e=t$가 존재해도 다른 $e\neq t$ candidate answer들이 멱살 잡고 score 값을 끌어내려줄 것이므로 크게 신경쓰지 않아도 괜찮다.
다시 본론으로 돌아와 위의 $score_w$를 사용하면 아래와 같이 candidate answer들의 분포를 알 수 있다.
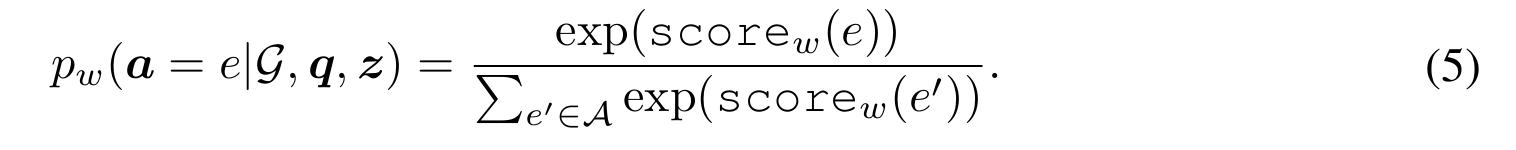
Optimization
이제 본격적으로 RG와 RP로 얻은 분포 데이터와 EM 알고리즘을 함께 활용하여 최적화하는 단계이다. 일단 Eq. (2)를 maximize 하는 방향에서 시작해 보자. 수식을 보면 기댓값이 있는데 $\hat{\textbf{z}}~p_\theta (\textbf{z}|\textbf{q})$를 sample 하여 근사 시켜주면 아래와 같이 식이 변한다.
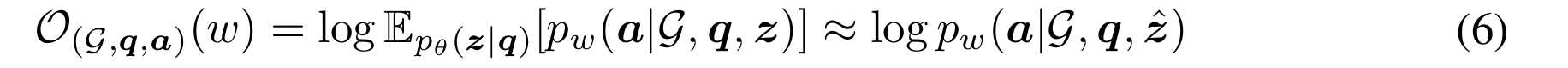
<E-step>
이 단계의 목적은 $\hat{\textbf{z}}$에서 $K$개의 high-quality rule들을 $\hat{\textbf{z}}_I$로 식별하는 것이다. 즉 우리는 일단 RG에서 제공받은 rule들 중에서 품질이 좋은 것들을 골라내야 하기 때문에 rule들에 대한 확률 분포가 필요하다.

$p_\theta$가 prior, $p_w$가 likelihood이므로 이 둘을 이용해 posterior를 계산할 수 있는 것이다. 즉 posterior에서 sampling을 하여 high-quality rule들을 획득할 수 있는 것이다. 하지만 위 수식에서 sampling 하는 것은 intractable partition function 때문에 힘들다. 따라서 아래의 수식으로 posterior가 근사 가능하다.


Partition function이 뭐고 뭐가 문제여서 근사했는가에 대해서는 appendix에서 근사 증명과 함께 설명하겠다.
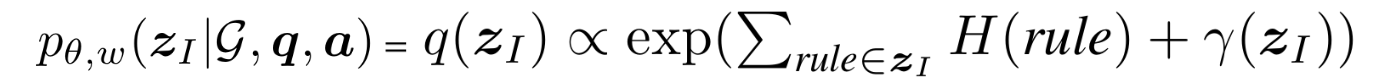
결국 log-posterior를 다항 분포 $q(\textbf{z}_I)$로 나타낼 수 있다. 이에 대한 증명도 appendix에 남긴다. 우리가 최종적으로 뽑고 싶은 high-quality rule을 $q(\textbf{z}_I)$에서 뽑는다고 해도 무방하며 이렇게 최종적으로 뽑힌 rule들을 $\hat{\textbf{z}_I}$이라고 하자. 즉 각 rule의 확률을 아래의 수식으로 구할 수 있는 것이다(rule에 영향을 받는 값이 $H$뿐이기 때문).

<M-step>
고품질의 rule들을 얻었기 때문에 이들로 RG를 update 해주면 된다. 즉 RG에 있는 $RNN_\theta$에게 $\hat{\textbf{z}_I}$에 해당하는 rule 생성을 강화하도록 피드백을 주면 되는 것이다.

결론적으로 high-quality rule을 생성하게끔 모델이 강화될 것이기 때문에 search space 감소와 전체적인 모델 성능 증가로 이어지게 된다.
추가적으로 RNNLogic+를 제시하는데, 이 모델은 RP에 전적으로 집중하는 모델이다.


생성된 high-quality rule이 3개가 있고 이에 따라 생성된 candidate answer도 3개라고 가정하면 각 rule에 대한 임베딩을 aggregate(이때 각 임베딩에 대한 weight는 $P(h,rule,e)$의 크기이다)하고 이렇게 나온 최종 임베딩을 MLP에 전파시켜 score을 얻는다(Aggregator의 종류는 PNA(Corso et al., 2020)이다). 이 score들로 Eq. (5)를 계산하는 데에 사용될 수 있다.
여기서 더 나아가 쿼리 자체에 대한 plausibility score를 계산할 수 있다.

이 두 변형 모델들은 실험에 포함시켜 평가한다.
Experiments
Dataset : FB15k-237, WN18RR, Kinship, UMLS. Kinship과 UMLS는 정형적인 split이 존재하지 않기 때문에 본 연구에서 무작위로 training(30%), validation(20%), testing(50%)으로 나눈다.

RNNLogic variants
1-1. RNNLogic w/o emb
$\phi_w(path)=1$로 고정, 즉 모든 경로에 같은 점수를 부여해 준다.
1-2. RNNLogic with emb
Architecture에서 설명한 방법대로 RotatE를 사용해 $\phi_w(path)$를 계산해 사용한다.
2-1. RNNLogic+ w/o emb
Eq. (10)를 이용한다. 즉 RP를 훈련하기 위해 RNNLogic에서 학습된 logic rule들만 이용한다.
2-2. RNNLogic+ with emb
Eq. (11)를 이용한다. 즉 RP를 훈련하기 위해 RNNLogic과 KG 임베딩을 모두 사용한다.
참고로 임베딩을 요구하는 variant들의 임베딩들은 pre-trained 된 값들이다.
Evaluation Metrics
각 test triplet $(h,r,t)$마다 2개의 쿼리 $(h,r,?)$와 $(t,r^{-1},?)$를 생성해 각 정답이 $t$, $h$인 상태로 평가한다. 이에 대한 이유는 FB15k, WN18에서 모델이 $r$을 train, $r^{-1}$을 test에 갖고 있더라도 모델이 training 과정에서 test에 있는 inverse relation을 기억한다는 점이 지적되었기 때문이다. 결국 inverse relation이 제거된 변형 데이터 FB15k-237, WN18RR이 제안되었다. 하지만 본 논문에서는 inverse relation을 test에서 사용하겠다고 해서 변형 데이터의 장점이 없어지는 것 아닌가 생각할 수 있다. 결론적으로 위의 행동은 문제가 되지 않는다, 왜냐하면 $(h,r,t)$가 train에 없다는 전제가 있기 때문이다.
MR(Mean Rank), MRR(Mean Reciprocal Rank), Hit@k을 사용하며 대부분의 연구에서 사용된 filtered setting($t$보다 rank가 높은 예측 entity 중에서 실제로 참인(데이터에 존재하는) triplet이 있다면 그 entity들을 제외하고 rank를 매김) 또한 적용한다.
논문에서 추가로 지적한 문제는 $t$와 같은 확률을 갖는 다른 entity들에 대한 처리이다. 즉 공동 순위 문제에 대한 해결방안이다. 과거에는 $t$보다 높은 순위에 놓인 entity의 개수가 $m$이라면 $t$의 rank를 $m+1$로 처리하였지만 이는 문제가 있다고(Sun et al. (2020)) 지적당한 바 있다. 따라서 같은 점수를 받은 entity의 개수가 $n$개 일 때 $t$의 rank를 $m+(n+1)/2$로 책정해 준다.
추가로 MINERVA(2018)과 MultiHopKG는 $(h,r,?)$만 사용하여 이들에 맞추기 위해 RNNLogic도 이들과 비교평가할 때는 $(h,r,?)$만 사용한다.
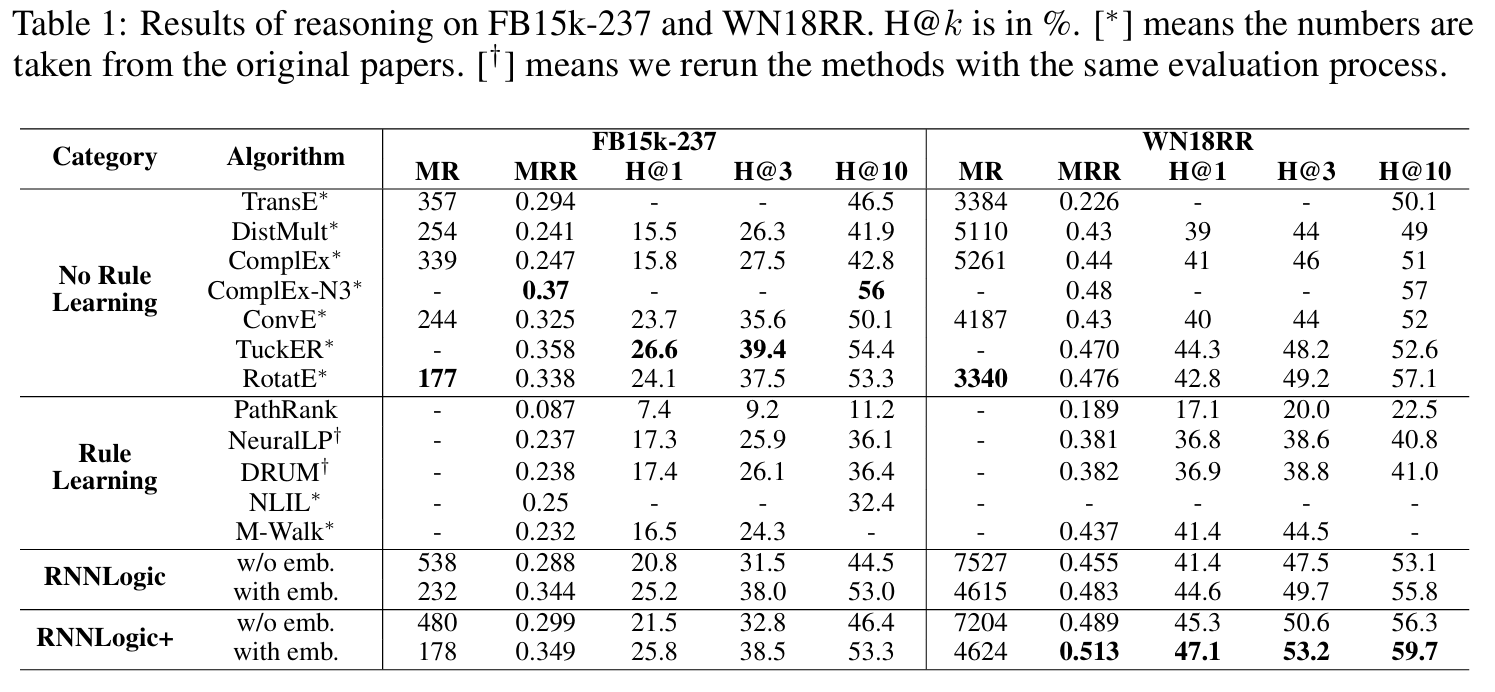

Experimental Setup
각 training triple $(h,r,t)$에 대해 $(t,r^{-1},h)$를 추가해 데이터를 확장해 $T$를 얻는다. 그리고 이를 통해 $p_{data}$(Eq. (2) 참고)에서 training instance를 뽑을 수 있게 하려면 쿼리로 지정할 데이터 $(h,r,t)$를 제외한 데이터를 background knowledge($G$)로 사용한다.

다음은 Kinship과 UMLS에 대한 결과이다.

아래는 적은 개수의 rule들 갖고도 높은 MRR 점수를 보임을 증명한다. 따라서 RNNLogic에서 학습한 rule은 high-quality임을 증명해 준다.

아래는 training 개수가 한정되어 있을 때 타 모델들과의 성능 비교이다.

Conclusion
RNNLogic은 Rule Generator와 이로부터 받은 rule들의 성능을 평가하는 Reasoning Predictor로 모델을 분할하여 EM 알고리즘에 기반한 모델을 제안하였다. 성능이 비교적 좋지만 한 가지 아쉬운 점은 pre-trained 임베딩을 사용함에 있어 원래 rule mining의 특성인 inductive setting에서 더욱이 멀어짐에 있다.
Appendix






